
| A. | 一个根,在(-∞,-$\frac{1}{3}$)内 | B. | 两个根,分别在(-∞,-$\frac{1}{3}$)、(0,+∞)内 | ||
| C. | 三个根,分别在(-∞,-$\frac{1}{3}$)、(-$\frac{1}{3}$,0),(1,+∞) | D. | 三个根,分别在(-∞,-$\frac{1}{3}$),(0,1),(1,+∞)内 |
分析 构造函数f(x)=-x3+x2+x-2,求函数的导数,判断函数的极值和单调性,利用函数极值的符号进行判断即可.
解答 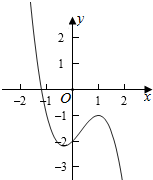 解:设f(x)=-x3+x2+x-2,
解:设f(x)=-x3+x2+x-2,
则f′(x)=-3x2+2x+1=-(x-1)(3x+1),
由f′(x)>0得-(x-1)(3x+1)>0,即(x-1)(3x+1)<0,
得-$\frac{1}{3}$<x<1,此时函数单调递增,
由f′(x)<0得,x<-$\frac{1}{3}$或>1,此时函数单调递减,
即当x=-$\frac{1}{3}$时,函数取得极小值,此时极小值为f(-$\frac{1}{3}$)=-$\frac{61}{54}$<0,
当x=1时,函数取得极大值,此时极大值为f(1)=-1<0,
当x→-∞时,f(x)>0,
故函数f(x)在(-∞,-$\frac{1}{3}$)上只有一个零点,
即方程-x3+x2+x-2=0只有一个根,根所在的区间为(-∞,-$\frac{1}{3}$),
故选:A,
点评 本题主要考查方程根的个数的判断,构造函数,求函数的导数,利用导数研究函数的极值是解决本题的关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
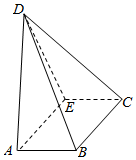 已知在底面为矩形的四棱锥D-ABCE中,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,二面角D-AE-C的平面角的正切值为-2.
已知在底面为矩形的四棱锥D-ABCE中,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,二面角D-AE-C的平面角的正切值为-2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
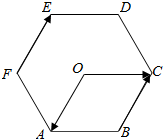
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
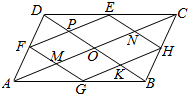
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com