练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．已知sinα=2cosα，求sin2α+2sinαcosα的值．

    分析 化简所求的表达式为正切函数的形式，代入求解即可．

    解答 解：∵sinα=2cosα，可得：tanα=2，
    ∴sin2α+2sinαcosα=$\frac{si{n}^{2}α+2sinαcosα}{si{n}^{2}α+co{s}^{2}α}$=$\frac{ta{n}^{2}α+2tanα}{ta{n}^{2}α+1}$=$\frac{4+2×2}{4+1}$=$\frac{8}{5}$．

    点评 本题考查三角函数化简求值，同角三角函数的基本关系式的应用，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    18．某几何体的三视图如图所示，则该几何体的体积是（　　）
    A．$\frac{4π}{3}$B．$\frac{5π}{3}$C．$2+\frac{2π}{3}$D．$4+\frac{2π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系的x轴的正半轴重合，设点O为坐标原点，直线l的参数方程为$\left\{\begin{array}{l}{x=t}\\{y=1+t}\end{array}\right.$ （参数t∈R），曲线C的极坐标方程为ρcos2θ=4sinθ．
    （1）求直线l的普通方程和曲线C的直角坐标方程；
    （2）设直线1与曲线C相交于A，B两点，求$\overrightarrow{OA}$•$\overrightarrow{OB}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．求1356和2400的最小公倍数271200．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．方程-x3+x2+x-2=0的根的分布情况是（　　）
    A．一个根，在（-∞，-$\frac{1}{3}$）内B．两个根，分别在（-∞，-$\frac{1}{3}$）、（0，+∞）内
    C．三个根，分别在（-∞，-$\frac{1}{3}$）、（-$\frac{1}{3}$，0），（1，+∞）D．三个根，分别在（-∞，-$\frac{1}{3}$），（0，1），（1，+∞）内

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．生于瑞士的数学巨星欧拉在1765年发表的《三角形的几何学》一书中有这样一个定理：“三角形的外心、垂心和重心都在同一直线上，而且外心和重心的距离是垂心和重心距离之半．”这就是著名的欧拉线定理．设△ABC中，设O、H、G分别是外心、垂心和重心，下列四个选项锥误的是（　　）
    A．HG=2OGB．$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$
    C．设BC边中点为D，则有AH=3ODD．S△ABG=S△BCG=S△ACG

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．在△ABC中，|$\overrightarrow{BC}$|=3，|$\overrightarrow{AC}$|=4，∠C=30°，则$\overrightarrow{BC}$•$\overrightarrow{CA}$=-6$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数f（x）=$\frac{1}{3}$x2+$\frac{1}{2}$ax2+bx，其导函数为f′（x），在区间[-1，1]内任取两个实数a，b，求方程f′（x）=0有实根的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

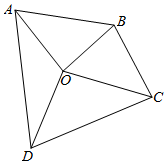    18．如图，为了测量学校操场四边形ABCD的周长和面积，在操场中间取一点O．测得OA=40m，OB=37m，OC=42m，OD=44m，且∠DOA=120°，∠AOB=80°，∠BOC=60°，∠COD=100°．
    （1）试求四边形ABCD的周长；
    （2）试求四边形ABCD的面积．（结果保留整数）

    查看答案和解析>>

    同步练习册答案