
| A. | HG=2OG | B. | $\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$ | ||
| C. | 设BC边中点为D,则有AH=3OD | D. | S△ABG=S△BCG=S△ACG |
分析 根据题意,画出图形,结合图形,利用欧拉线定理得出选项A正确;
根据三角形的重心性质得出选项B正确;
根据△AHG∽△DOG,判断选项C错误;
求出S△BGC=S△AGC=S△AGB=$\frac{1}{3}$S△ABC,判断选项D正确.
解答 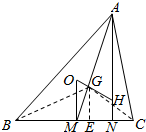 解:△ABC中,O、H、G分别是外心、垂心和重心,
解:△ABC中,O、H、G分别是外心、垂心和重心,
画出图形,如图所示;
对于A,根据欧拉线定理得HG=2OG,选项A正确;
对于B,根据三角形的重心性质得$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,选项B正确;
对于C,∵AH∥OD,∴△AHG∽△DOG,∴$\frac{AH}{OD}$=$\frac{AG}{DG}$=2,∴AH=2OD,选项C错误;
对于D,过点G作GE⊥BC,垂足为E,则$\frac{GE}{AN}$=$\frac{DG}{DA}$=$\frac{1}{3}$,
∴△BGC的面积为S△BGC=$\frac{1}{2}$×BC×GE=$\frac{1}{2}$×BC×$\frac{1}{3}$×AN=$\frac{1}{3}$S△ABC;
同理,S△AGC=S△AGB=$\frac{1}{3}$S△ABC,选项D正确.
故选:C.
点评 本题考查了三角形中的重心,外心与垂心的应用问题,也考查了分析问题与解答问题的能力,是综合性题目


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 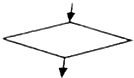 | B. | 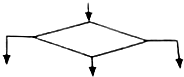 | ||
| C. | 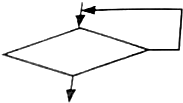 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
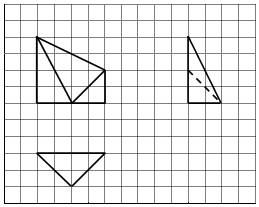 如图,网格纸上每个正方形小格的边长为1,图中粗线画出的是某多面体的三视图,则该几何体的表面中互相垂直的平面有( )
如图,网格纸上每个正方形小格的边长为1,图中粗线画出的是某多面体的三视图,则该几何体的表面中互相垂直的平面有( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
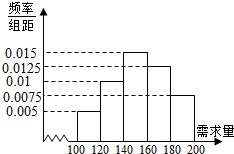 大学生小李毕业后自主创业,买了一辆小型卡车,运输农产品.在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.根据以往市场调查,得到葡萄收获季节市场需求量的直方图,如图所示,今年葡萄收获的季节,小季给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,Y(单位:元)表示今年葡萄销售的利润.
大学生小李毕业后自主创业,买了一辆小型卡车,运输农产品.在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.根据以往市场调查,得到葡萄收获季节市场需求量的直方图,如图所示,今年葡萄收获的季节,小季给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,Y(单位:元)表示今年葡萄销售的利润.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{9}$ | B. | $\frac{π}{9}$ | C. | $\frac{π}{18}$ | D. | $\frac{π}{36}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com