
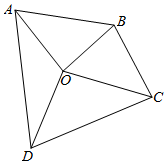
 如图,为了测量学校操场四边形ABCD的周长和面积,在操场中间取一点O.测得OA=40m,OB=37m,OC=42m,OD=44m,且∠DOA=120°,∠AOB=80°,∠BOC=60°,∠COD=100°.
如图,为了测量学校操场四边形ABCD的周长和面积,在操场中间取一点O.测得OA=40m,OB=37m,OC=42m,OD=44m,且∠DOA=120°,∠AOB=80°,∠BOC=60°,∠COD=100°.分析 (1)在四个小三角形中分别使用余弦定理求出操场的四条边,
(2)分别求出四个小三角形的面积.
解答 解:(1)在△AOB中,由余弦定理得AB2=OA2+OB2-2OA•OB•cos∠AOB=1600+1369-2×40×37×0.17=2465.80,∴AB≈49.66.
在△AOD中,由余弦定理得AD2=OA2+OD2-2OA•OD•cos∠AOD=1600+1936-2×40×44×(-$\frac{1}{2}$)=5296,∴AD≈72.77.
在△BOC中,由余弦定理得BC2=OB2+OC2-2OB•OC•cos∠BOC=1369+1764-2×37×42×$\frac{1}{2}$=1579,∴BC≈39.74.
在△COD中,由余弦定理得CD2=OC2+OD2-2OC•OD•cos∠COD=1764+1936-2×42×44×(-0.17)=4328.3,∴CD≈65.79.
∴AB+BC+CD+AD=49.66+72.77+39.74+65.79=227.96≈228(m).
∴四边形ABCD的周长约为228m.
(2)S△AOB=$\frac{1}{2}$•OA•OB•sin∠AOB=$\frac{1}{2}$×40×37×0.98≈725.2,S△BOC=$\frac{1}{2}$•OC•OB•sin∠COB=$\frac{1}{2}×$42×37×$\frac{\sqrt{3}}{2}$≈672.9,
S△COD=$\frac{1}{2}$•OC•OD•sin∠COD=$\frac{1}{2}$×42×44×0.98≈905.5,S△AOD=$\frac{1}{2}$•OA•OD•sin∠AOD=$\frac{1}{2}×$40×44×$\frac{\sqrt{3}}{2}$≈762.1.
∴S△AOB+S△BOC+S△COD+S△AOD=725.2+672.9+905.5+762.1≈3066.
∴四边形ABCD的面积约为3066m2.
点评 本题考查了余弦定理,解三角形的应用,属于中档题.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | tanα=-$\frac{sinα}{cosα}$ | B. | cosα=-$\sqrt{1-si{n}^{2}α}$ | C. | sinα=-$\sqrt{1-co{s}^{2}α}$ | D. | tanα=$\frac{cosα}{sinα}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
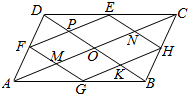
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{9}$ | B. | $\frac{π}{9}$ | C. | $\frac{π}{18}$ | D. | $\frac{π}{36}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com