
分析 (1)设椭圆C的方程为:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1,a>b>0,由已知得$\left\{\begin{array}{l}{\frac{2}{{a}^{2}}+\frac{1}{{b}^{2}}=1}\\{{a}^{2}={b}^{2}+2}\end{array}\right.$,由此能求出椭圆C的方程.
(2)由已知得|MN|=$\sqrt{3}$•|x1-x2|=$\frac{\sqrt{6}}{2}$•$\sqrt{8-{m}^{2}}$,P到直线l的距离d=$\frac{|m|}{\sqrt{3}}$,由此能求出当m=±2时,△PMN的面积最大值为$\sqrt{2}$.
解答 解:(1)∵抛物线x2=4$\sqrt{2}$y的焦点为(0,$\sqrt{2}$),
∴设椭圆C的方程为:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1,a>b>0,
∵点P(1,$\sqrt{2}$)是椭圆C是一点,一个焦点与抛物线x2=4$\sqrt{2}$y的焦点相同,
∴$\left\{\begin{array}{l}{\frac{2}{{a}^{2}}+\frac{1}{{b}^{2}}=1}\\{{a}^{2}={b}^{2}+2}\end{array}\right.$,解得a2=4,b2=2,
∴椭圆C的方程为$\frac{{y}^{2}}{4}+\frac{{x}^{2}}{2}=1$.
(2)设直线l的方程为y=$\sqrt{2}$x+m,
与椭圆方程联立,得4x2+2$\sqrt{2}$mx+m2-4=0,
由△=-8m2+64>0,得$\sqrt{2}<m<2\sqrt{2}$,
设M(x1,y1),N(x2,y2),则x1+x2=-$\frac{\sqrt{2}}{2}$m,x1x2=$\frac{{m}^{2}-4}{4}$,
∴|MN|=$\sqrt{3}$•|x1-x2|=$\frac{\sqrt{6}}{2}$•$\sqrt{8-{m}^{2}}$,
∵P到直线l的距离d=$\frac{|m|}{\sqrt{3}}$,
∴△PMN的面积S=$\frac{\sqrt{2}}{4}•\sqrt{(8-{m}^{2}){m}^{2}}$≤$\sqrt{2}$,
当且仅当8-m2=m2,即m=±2时取等号,
∴当m=±2时,△PMN的面积最大,最大值为$\sqrt{2}$.
点评 本题考查椭圆方程的求法,考查三角形面积最大值的求法,解题时要认真审题,注意椭圆弦长公式的合理运用.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,抛物线y=$\frac{1}{4}$x2-x+1的顶点A在x轴上,与y轴交于B,延长AB至C,使BC=2AB,将抛物线向左平移n个单位,使抛物线与线段AC总有两个交点,求n的取值范围.
如图,抛物线y=$\frac{1}{4}$x2-x+1的顶点A在x轴上,与y轴交于B,延长AB至C,使BC=2AB,将抛物线向左平移n个单位,使抛物线与线段AC总有两个交点,求n的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
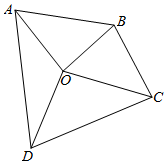 如图,为了测量学校操场四边形ABCD的周长和面积,在操场中间取一点O.测得OA=40m,OB=37m,OC=42m,OD=44m,且∠DOA=120°,∠AOB=80°,∠BOC=60°,∠COD=100°.
如图,为了测量学校操场四边形ABCD的周长和面积,在操场中间取一点O.测得OA=40m,OB=37m,OC=42m,OD=44m,且∠DOA=120°,∠AOB=80°,∠BOC=60°,∠COD=100°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com