
【题目】已知奇函数f(x)=ax+ka-x,(a>0且a≠1,k∈R).
(1)求实数k的值;
(2)是否存在实数a,使函数y=(f(x)+2)ax在[-1,1]上的最大值为7?
【答案】(1)k=-1(2)存在a=![]() 或a=2,使函数y=(f(x)+2)ax在[-1,1]上的最大值为7
或a=2,使函数y=(f(x)+2)ax在[-1,1]上的最大值为7
【解析】
(1)f(x)=ax+ka-x为奇函数,则f(0)=1+k=0,进而求解;
(2)由(1)知y=(f(x)+2)ax=(ax)2+2ax-1,设ax=t,(t>0),则g(t)=t2+2t-1进而求解.
解:(1)f(x)=ax+ka-x为奇函数,则f(0)=1+k=0,解得k=-1;
(2)由(1)知f(x)=ax-a-x,y=(f(x)+2)ax=(ax-a-x+2)ax=(ax)2+2ax-1,
设ax=t,(t>0),则g(t)=t2+2t-1,令g(t)=7,即t2+2t-1=7,解得t=2或t=-4(舍)
∴ax=2,若0<a<1,则y=ax在[-1,1]为减函数,∴a=![]() ;若a>1,则y=ax在[-1,1]为增函数,∴a=2;
;若a>1,则y=ax在[-1,1]为增函数,∴a=2;
综上,存在a=![]() 或a=2使函数y=(f(x)+2)ax在[-1,1]上的最大值为7.
或a=2使函数y=(f(x)+2)ax在[-1,1]上的最大值为7.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
【题目】下表中的数表为“森德拉姆筛”(森德拉姆,东印度学者),其特点是每行每列都成等差数列.
2 | 3 | 4 | 5 | 6 | 7 | … |
3 | 5 | 7 | 9 | 11 | 13 | … |
4 | 7 | 10 | 13 | 16 | 19 | … |
5 | 9 | 13 | 17 | 21 | 25 | … |
6 | 11 | 16 | 21 | 26 | 31 | … |
7 | 13 | 19 | 25 | 31 | 37 | … |
… | … | … | … | … | … | … |
在上表中,2017出现的次数为( )
A. 18 B. 36 C. 48![]() D. 72
D. 72
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.在极坐标系中有射线
轴的正半轴为极轴建立极坐标系.在极坐标系中有射线![]() 和曲线
和曲线![]() .
.
(1)判断射线![]() 和曲线
和曲线![]() 公共点的个数;
公共点的个数;
(2)若射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且满足
两点,且满足![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
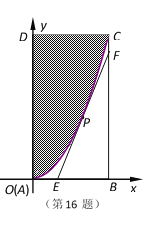
【题目】国务院批准从2009年起,将每年8月8日设置为“全民健身日”,为响应国家号召,各地利用已有土地资源建设健身场所.如图,有一个长方形地块![]() ,边
,边![]() 为
为![]() ,
,![]() 为
为![]() .地块的一角是草坪(图中阴影部分),其边缘线
.地块的一角是草坪(图中阴影部分),其边缘线![]() 是以直线
是以直线![]() 为对称轴,以
为对称轴,以![]() 为顶点的抛物线的一部分.现要铺设一条过边缘线
为顶点的抛物线的一部分.现要铺设一条过边缘线![]() 上一点
上一点![]() 的直线型隔离带
的直线型隔离带![]() ,
,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上(隔离带不能穿越草坪,且占地面积忽略不计),将隔离出的△
上(隔离带不能穿越草坪,且占地面积忽略不计),将隔离出的△![]() 作为健身场所.则△
作为健身场所.则△![]() 的面积为
的面积为![]() 的最大值为____________(单位:
的最大值为____________(单位:![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的产品的生产线上随机抽取 件产品,测量这批产品的一项质量指标值,由测量结果得如图所示的频率分布直方图:
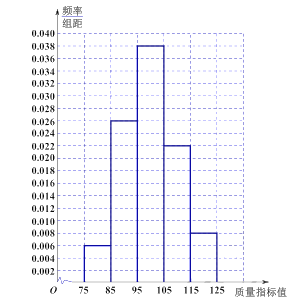
(Ⅰ) 估计这批产品质量指标值的样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ) 若该种产品的等级及相应等级产品的利润(每件)参照以下规则(其中![]() 为产品质量指标值):
为产品质量指标值):
当![]() , 该产品定为一等品,企业可获利 200 元;
, 该产品定为一等品,企业可获利 200 元;
当![]() 且
且![]() ,该产品定为二等品,企业可获利 100 元;
,该产品定为二等品,企业可获利 100 元;
当![]() 且
且![]() ,该产品定为三等品,企业将损失 500 元;
,该产品定为三等品,企业将损失 500 元;
否则该产品定为不合格品,企业将损失 1000 元.
(ⅰ)若测得一箱产品(5 件)的质量指标数据分别为:76、85、93、105、112,求该箱产品的利润;
(ⅱ)设事件![]() ;事件
;事件![]() ;事件
;事件![]() . 根据经验,对于该生产线上的产品,事件
. 根据经验,对于该生产线上的产品,事件![]() 发生的概率分别为0.6826、0.9544、0.9974.根据以上信息,若产品预计年产量为10000件,试估计该产品年获利情况.(参考数据:
发生的概率分别为0.6826、0.9544、0.9974.根据以上信息,若产品预计年产量为10000件,试估计该产品年获利情况.(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年元旦假期,高三的8名同学准备拼车去旅游,其中![]() 班、
班、![]() 班,
班,![]() 班、
班、![]() 班每班各两名,分乘甲乙两辆汽车,每车限坐4名同学
班每班各两名,分乘甲乙两辆汽车,每车限坐4名同学![]() 乘同一辆车的4名同学不考虑位置
乘同一辆车的4名同学不考虑位置![]() ,其中
,其中![]() 班两位同学是孪生姐妹,需乘同一辆车,则乘坐甲车的4名同学中恰有2名同学是来自同一个班的乘坐方式共有
班两位同学是孪生姐妹,需乘同一辆车,则乘坐甲车的4名同学中恰有2名同学是来自同一个班的乘坐方式共有![]()
![]()
A. 18种 B. 24种 C. 48种 D. 36种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为( )

(A)![]() (B)-
(B)-![]() (C)
(C)![]() (D)-
(D)-![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com