
【题目】在平面直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.在极坐标系中有射线
轴的正半轴为极轴建立极坐标系.在极坐标系中有射线![]() 和曲线
和曲线![]() .
.
(1)判断射线![]() 和曲线
和曲线![]() 公共点的个数;
公共点的个数;
(2)若射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且满足
两点,且满足![]() ,求实数
,求实数![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,且
为正方形,且![]() ,其中
,其中![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,动点
的中点,动点![]() 在线段
在线段![]() 上运动时,下列四个结论:①
上运动时,下列四个结论:①![]() ;②
;②![]() ;③
;③![]() 面
面![]() ;④
;④![]() 面
面![]() ,
,
其中恒成立的为( )

A. ①③ B. ③④ C. ①④ D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校做了一次关于“感恩父母”的问卷调查,从8~10岁,11~12岁,13~14岁,15~16岁四个年龄段回收的问卷依次为:120份,180份,240份,x份.因调查需要,从回收的问卷中按年龄段分层抽取容量为300的样本,其中在11~12岁学生问卷中抽取60份,则在15~16岁学生中抽取的问卷份数为( )
A.60 B.80 C.120 D.180
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个不同点.
上的两个不同点.
(1)若![]() ,且点
,且点![]() 所在直线方程为
所在直线方程为![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 的斜率之积为
的斜率之积为![]() ,线段
,线段![]() 上有一点
上有一点![]() 满足
满足![]() ,连接
,连接![]() 并廷长交椭圆
并廷长交椭圆![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
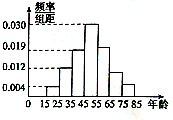
【题目】某购物中心为了了解顾客使用新推出的某购物卡的顾客的年龄分布情况,随机调查了![]() 位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间
位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间![]() 内的频率之比为
内的频率之比为![]() .
.
(1) 求顾客年龄值落在区间![]() 内的频率;
内的频率;
(2) 拟利用分层抽样从年龄在![]() 的顾客中选取
的顾客中选取![]() 人召开一个座谈会,现从这
人召开一个座谈会,现从这![]() 人中选出
人中选出![]() 人,求这两人在不同年龄组的概率.
人,求这两人在不同年龄组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)=ax+ka-x,(a>0且a≠1,k∈R).
(1)求实数k的值;
(2)是否存在实数a,使函数y=(f(x)+2)ax在[-1,1]上的最大值为7?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x-a|+bx.
(1)若a=2,且f(x)是R上的增函数,求实数b的取值范围;
(2)当b=0时,若关于x的方程f(x)=x+1有三个实根,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为R,如果存在函数g(x),使得f(x)≥g(x)对于一切实数x都成立,那么称g(x)为函数f(x)的一个承托函数.已知函数f(x)=ax2+bx+c的图象经过点(-1,0).
(1)若a=1,b=2.写出函数f(x)的一个承托函数(结论不要求证明);
(2)判断是否存在常数a,b,c,使得y=x为函数f(x)的一个承托函数,且f(x)为函数![]() 的一个承托函数?若存在,求出a,b,c的值;若不存在,说明理由.
的一个承托函数?若存在,求出a,b,c的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com