
 平面ABCD,E,F分别为MA,DC的中点,求证:
平面ABCD,E,F分别为MA,DC的中点,求证:
 平面BND.
平面BND.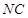 的中点
的中点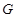 ,连接
,连接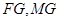 ,欲证
,欲证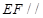 平面
平面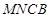 ,只要证
,只要证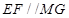
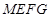 是平行四边形即可,事实上,由于
是平行四边形即可,事实上,由于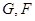 分别是
分别是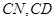 的中点,易知
的中点,易知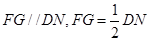 另一方面又有
另一方面又有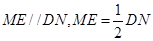 ,所以FG与ME平行且相等,四边形
,所以FG与ME平行且相等,四边形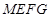 是平行四边形,问题得证.
是平行四边形,问题得证.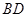 、
、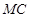 ,欲证
,欲证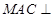 平面
平面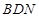 ,只要证
,只要证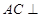 平面
平面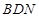 ,即证
,即证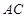 与平面
与平面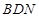 内的两条相交直线
内的两条相交直线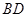 、
、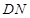 都垂直;由菱形
都垂直;由菱形 易知
易知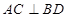 ;另外,由平面
;另外,由平面 平面
平面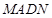
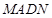 易证
易证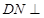 平面
平面 ,进而有
,进而有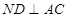 ,所以问题得证.
,所以问题得证.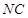 的中点
的中点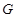 ,连接
,连接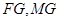 ,
,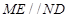 且
且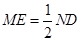 ,
, 、
、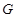 分别为
分别为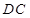 、
、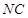 的中点,
的中点,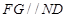 且
且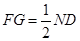 , 2分
, 2分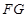 与
与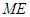 平行且相等,所以四边形
平行且相等,所以四边形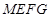 是平行四边形,
是平行四边形,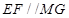 , 4分
, 4分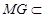 平面
平面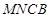 ,
,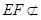 平面
平面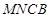 ,
,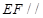 平面
平面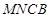 6分
6分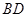 、
、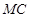 ,因为四边形
,因为四边形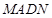 是矩形,
是矩形,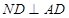 ,又因为平面
,又因为平面 平面
平面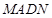
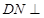 平面
平面 8分
8分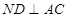
 是菱形,所以
是菱形,所以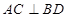
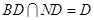 ,所以
,所以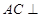 平面
平面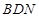 10分
10分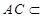 平面
平面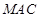
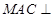 平面
平面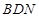 12分
12分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
 ,四边形ACFE是矩形,且平面
,四边形ACFE是矩形,且平面 平面ABCD,点M在线段EF上.
平面ABCD,点M在线段EF上. 平面ACFE;
平面ACFE;
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 A1B1C1D1中,AD∥BC,AD⊥AB,AB=
A1B1C1D1中,AD∥BC,AD⊥AB,AB= ,AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
,AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段 上,且
上,且 ,设面
,设面 面MPQ=
面MPQ= ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )
 面ABCD
面ABCD AC
AC 不是定直线
不是定直线查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 平面
平面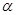 ,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,则线段AB与EF在平面
,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,则线段AB与EF在平面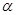 上的射影所成角余弦值的范围是( )
上的射影所成角余弦值的范围是( )A.[0, ] ] | B.[ ,1] ,1] | C.[ ,1] ,1] | D.[ , , ] ] |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 中,
中,

 ,
, ,
, ,
, ,将
,将 沿对角线
沿对角线 折起.设折起后点
折起.设折起后点 的位置为
的位置为 ,并且平面
,并且平面
 平面
平面 .给出下面四个命题:
.给出下面四个命题: ;②三棱锥
;②三棱锥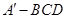 的体积为
的体积为 ;③
;③
 平面
平面 ;④平面
;④平面 平面
平面 .
.
| A.①② | B.③④ | C.①③ | D.②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com