
分析 (1)根据向量的数量积运算即可,
(2)根据向量的模和二次函数的性质求出x的值,再根据向量的夹角的公式计算即可.
解答 解:(1)∵向量$\overrightarrow a,\overrightarrow b$的夹角为135°,且$|\overrightarrow a|=\sqrt{2},|\overrightarrow b|=2$,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos135°=$\sqrt{2}$×2×(-$\frac{\sqrt{2}}{2}$)=-2,
(2)设$\overrightarrow c=x\overrightarrow a-\overrightarrow b(x∈R)$,
∴|$\overrightarrow{c}$|2=x2${\overrightarrow{a}}^{2}$-2x$\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=2x2+4x+4=2(x+1)2+2≥2,当且仅当x=-1时取等号,
∴$\overrightarrow{c}$=$\overrightarrow{a}$+$\overrightarrow{b}$,
∴$\overrightarrow{c}$•$\overrightarrow{b}$=$\overrightarrow{b}$($\overrightarrow{a}$+$\overrightarrow{b}$)=$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=-2+4=2
当$|\overrightarrow c|$取得最小值为$\sqrt{2}$,
设向量$\overrightarrow c$与$\overrightarrow b$夹角为θ,
∴cosθ=$\frac{\overrightarrow{c}•\overrightarrow{b}}{|\overrightarrow{c}|•|\overrightarrow{b}|}$=$\frac{2}{2×\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∵0°≤θ≤180°,
∴θ=45°
点评 本题主要考查两个向量的数量积的定义以及向量的夹角公式,求向量的模的方法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 一条直线和一个圆 | B. | 一条直线和半个圆 | ||
| C. | 两条射线和一个圆 | D. | 一条线段和半个圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
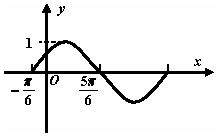 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象如图所示,则下列关于函数 f (x)的说法中正确的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象如图所示,则下列关于函数 f (x)的说法中正确的是( )| A. | 对称轴方程是x=$\frac{π}{6}$+kπ(k∈Z) | B. | 对称中心坐标是($\frac{π}{3}$+kπ,0)(k∈Z) | ||
| C. | 在区间(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递增 | D. | 在区间(-π,-$\frac{2π}{3}$)上单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a?α,b?β,α∥β | B. | a∥α,b?β | C. | a⊥α,b⊥α | D. | a⊥α,b?α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{3}$-y2=1 | B. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{6}$=1 | C. | $\frac{{y}^{2}}{3}$-x2=1 | D. | $\frac{{y}^{2}}{6}$-$\frac{{x}^{2}}{2}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-25,-$\frac{1}{2}$] | B. | [-5,-$\frac{1}{2}$] | C. | [-25,-1] | D. | [-5,-1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com