
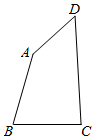
 如图,在凸四边形ABCD中,C,D为定点,CD=$\sqrt{3}$,A,B为动点,满足AB=BC=DA=1.
如图,在凸四边形ABCD中,C,D为定点,CD=$\sqrt{3}$,A,B为动点,满足AB=BC=DA=1.分析 (1)连接BD,在三角形BCD与三角形ABD中,分别利用余弦定理表示出BD2,将C的度数代入求出cosA的值即可;
(2)利用三角形面积公式表示出S与T,进而表示出S2+T2,利用同角三角函数间的基本关系及二次函数性质求出范围即可.
解答 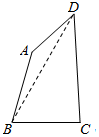 解:(1)连接BD,由余弦定理得:
解:(1)连接BD,由余弦定理得:
在△BCD中,BD2=BC2+CD2-2•BC•CDcosC=4-2$\sqrt{3}$cosC,
在△ABD中,BD2=AB2+AD2-2AB•ADcosA=2-2cosA,
∴4-2$\sqrt{3}$cosC=2-2cosA,即cosA=$\sqrt{3}$cosC-1,
∵C=$\frac{π}{4}$,
∴cosA=$\frac{\sqrt{6}}{2}$-1;
(2)∵S=$\frac{1}{2}$BC•CD•sinC=$\frac{\sqrt{3}}{2}$sinC,T=$\frac{1}{2}$AB•ADsinA=$\frac{1}{2}$sinA,
∴S2+T2=$\frac{3}{4}$sin2C+$\frac{1}{4}$sin2A=$\frac{3}{4}$(1-cos2C)+$\frac{1}{4}$(1-cos2A)
由余弦定理可得BD2=1+1-2cosA=1+3-2$\sqrt{3}$cosC,
可得cosA=$\sqrt{3}$cosC-1,
∴S2+T2=-$\frac{3}{2}$cos2C+$\frac{\sqrt{3}}{2}$cosC+$\frac{3}{4}$=-$\frac{3}{2}$(cosC-$\frac{\sqrt{3}}{6}$)2+$\frac{7}{8}$,
由题意易知,C∈(300,900),
∴cosC∈(0,$\frac{\sqrt{3}}{2}$),
∴S2+T2∈($\frac{3}{4}$,$\frac{7}{8}$].
点评 此题考查了正弦、余弦定理,二次函数性质,三角形面积公式,以及同角三角函数间的基本关系,熟练掌握定理及公式是解本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${y^2}=\frac{{16\sqrt{3}}}{3}x$ | B. | ${y^2}=\frac{{8\sqrt{3}}}{3}x$ | C. | y2=16x | D. | y2=8x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{3}{4}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
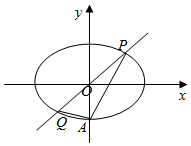 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点A(0,-1),且离心率为$\frac{\sqrt{2}}{2}$.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点A(0,-1),且离心率为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 不及格 | 及格 | 总计 | |
| 甲班 | 10 | 35 | 45 |
| 乙班 | 7 | 38 | 45 |
| 总计 | 17 | 73 | 90 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com