
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{3}{4}$ | D. | -1 |
分析 根据题意可知C在线段AB上,从而得出|$\overrightarrow{OC}$|的范围,用$\overrightarrow{OM}$,$\overrightarrow{ON}$,$\overrightarrow{OC}$表示出$\overrightarrow{CM},\overrightarrow{CN}$,代入数量积公式得出关于|$\overrightarrow{OC}$|的式子,根据|$\overrightarrow{OC}$|的范围得出答案.
解答  解:∵$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+(1-λ)$\overrightarrow{OB}$,
解:∵$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+(1-λ)$\overrightarrow{OB}$,
∴点C在线段AB上,即A,B,C三点共线.
∵OA=OB=1,∠AOB=120°,
∴O到直线AB的距离d=$\frac{1}{2}$.
∴$\frac{1}{2}≤$|$\overrightarrow{OC}$|<1.
∴$\overrightarrow{CM}$•$\overrightarrow{CN}$=($\overrightarrow{OM}-\overrightarrow{OC}$)•($\overrightarrow{ON}-\overrightarrow{OC}$)=$\overrightarrow{OM}•\overrightarrow{ON}$-($\overrightarrow{OM}+\overrightarrow{ON}$)$•\overrightarrow{OC}$+${\overrightarrow{OC}}^{2}$.
∵MN是单位圆O的直径,
∴$\overrightarrow{OM}•\overrightarrow{ON}$=-1,$\overrightarrow{OM}+\overrightarrow{ON}$=$\overrightarrow{0}$,
∴$\overrightarrow{CM}$•$\overrightarrow{CN}$=-1+${\overrightarrow{OC}}^{2}$.
∴-$\frac{3}{4}$≤$\overrightarrow{CM}$•$\overrightarrow{CN}$<0.
则$\overrightarrow{CM}$•$\overrightarrow{CN}$的最小值为-$\frac{3}{4}$,
故选:C.
点评 本题考查了平面向量的数量积运算,向量线性运算的性质与几何意义,利用数形结合以及转化法是解决本题的关键.属于中档题.本题也可以使用坐标法进行求解.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:解答题
| 身高(单位:cm) | [180,185) | [185,190) | [190,195) | [195,200) | [200,205) | [205,210] |
| 人数 | 2 | 3 | 3 | 2 | 1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 现有4种不同的颜色为公民基本道德规范四个主题词(如图)涂色,要求相邻的词语涂色不同,则不同的涂法种数为( )
现有4种不同的颜色为公民基本道德规范四个主题词(如图)涂色,要求相邻的词语涂色不同,则不同的涂法种数为( )| A. | 27 | B. | 54 | C. | 108 | D. | 144 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
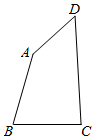 如图,在凸四边形ABCD中,C,D为定点,CD=$\sqrt{3}$,A,B为动点,满足AB=BC=DA=1.
如图,在凸四边形ABCD中,C,D为定点,CD=$\sqrt{3}$,A,B为动点,满足AB=BC=DA=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 6 | C. | 2或1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com