
·ÖÎö Éè$\overrightarrow{OA}=\overrightarrow{a}$£¬$\overrightarrow{OB}=\overrightarrow{b}$£¬$\overrightarrow{OC}=2\overrightarrow{b}$£¬Ộ¡÷OABΪ±ß³¤Îª2µÄµÈ±ßÈư½ÇĐΣ¬ÀûÓĂÓàÏ̉¶¨Àí¼ÆËă³öAC¼´Îª|2$\overrightarrow{b}-\overrightarrow{a}$|£®
½â´đ 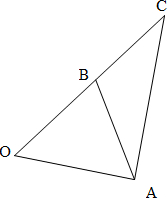 ½â£ºÉè$\overrightarrow{OA}=\overrightarrow{a}$£¬$\overrightarrow{OB}=\overrightarrow{b}$£¬Ộ$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$=$\overrightarrow{b}-\overrightarrow{a}$£®
½â£ºÉè$\overrightarrow{OA}=\overrightarrow{a}$£¬$\overrightarrow{OB}=\overrightarrow{b}$£¬Ộ$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$=$\overrightarrow{b}-\overrightarrow{a}$£®
¡ß|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=2£¬
¡à¡÷OABÊDZ߳¤Îª2µÄµÈ±ßÈư½ÇĐΣ¬
ÑÓ³¤OBµ½C£¬Ê¹µĂOC=2OB£¬Ộ$\overrightarrow{OC}=2\overrightarrow{OB}=2\overrightarrow{b}$£¬
¡à$\overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA}=2\overrightarrow{b}-\overrightarrow{a}$£¬
ÔÚ¡÷ABCÖĐ£¬ÓÉÓàÏ̉¶¨ÀíµĂAC2=AB2+BC2-2AB•BCcos120¡ă=12£®
¡àAC=2$\sqrt{3}$£®
¹Ê´đ°¸Îª£º2$\sqrt{3}$£®
µăÆÀ ±¾̀⿼²éÁËƽĂæỊ̈Á¿ÏßĐÔÔËËăµÄ¼¸ºÎ̉ẩ壬ÊôÓÚÖеµ̀⣮


 ÅàÓÅºĂ¾íµ¥Ôª¼ÓÆÚÄ©¾íϵÁĐ´đ°¸
ÅàÓÅºĂ¾íµ¥Ôª¼ÓÆÚÄ©¾íϵÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | 3¡Ê{y|y=x2+¦Đ£¬x¡ÊR} | B£® | {£¨a£¬b£©}={£¨b£¬a£©} | ||
| C£® | {£¨x£¬y£©|x2-y2=1}⊆{£¨x£¬y£©|£¨x2-y2£©2=1} | D£® | {x¡ÊR|x2-2=0}=∅ |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | Æ溯Êư | B£® | żº¯Êư | ||
| C£® | ¼ÈÊÇÆ溯ÊưÓÖÊÇżº¯Êư | D£® | ¼È²»ÊÇÆ溯ÊưÓÖ²»ÊÇżº¯Êư |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | 1 | B£® | 2 | C£® | 3 | D£® | 4 |
²é¿´´đ°¸ºÍ½âÎö>>
¹ú¼ÊÑ§Đ£ÓÅÑ¡ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com