
分析 (Ⅰ)根据函数的极值,求出m的值,得到f(x)的表达式,从而求出f(x)的单调区间即可
(Ⅱ)当m≤2,x∈(0,+∞)时,ex-m≥ex-2,又ex≥x+1,从而ex-m≥ex-2≥x-1,取函数h(x)=x-1-ln(2x)(x>0),h′(x)=1-$\frac{1}{x}$,由此利用导性质能证明f(x)>ln3.
解答 解:(Ⅰ)∵f(x)=ex-m+ln$\frac{3}{x}$,
∴x>0,${f}^{'}(x)={e}^{x-m}-\frac{1}{x}$,
∵x=1是函数f(x)的极值点,
∴f′(1)=e1-m-1=0,解得m=1.
∴f(x)=${e}^{x-1}+ln\frac{3}{x}$,定义域为x>0,
${f}^{'}(x)={e}^{x-1}-\frac{1}{x}$,${f}^{''}(x)={e}^{x-1}+\frac{1}{{x}^{2}}$>0,
∴x=1是f′(x)=0的唯一零点,
∴当x∈(0,1)时,f′(x)<0,函数f(x)单调递减;
当x∈(1,+∞)时,f′(x)>0,函数f(x)单调递增.
(Ⅱ)证明:当m≤2,x∈(0,+∞)时,ex-m≥ex-2,
又ex≥x+1,∴ex-m≥ex-2≥x-1.
取函数h(x)=x-1+ln$\frac{3}{x}$,(x>0),h′(x)=1-$\frac{1}{x}$,
当0<x<1时,h′(x)<0,h(x)单调递减;当x>1时,h′(x)>0,h(x)单调递增,
得函数h(x)在x=1时取唯一的极小值即最小值为h(1)=ln3.
∴f(x)=ex-m+ln$\frac{3}{x}$≥ex-2-ln$\frac{3}{x}$≥x-1-ln$\frac{3}{x}$≥ln3,
而上式三个不等号不能同时成立,故f(x)>ln3.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题、属于中档题.


科目:高中数学 来源: 题型:解答题
| 房屋面积(平方米) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>2 | B. | a>3,-3<b<-1 | ||
| C. | a<0<b,a+b>0 | D. | a>2,-2<b<0,a-b>4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{25}{3}$ | C. | -89 | D. | $\frac{17}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
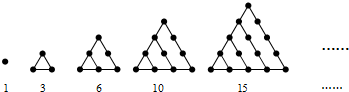
| A. | 35 | B. | 36 | C. | 45 | D. | 55 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com