
分析 设x=logba,得到f(x)=${2}^{x}+\frac{1}{{x}^{2}}-\frac{17}{4}$,f(2)=0,利用导数性质求出f(x)在定义域内是单调递增函数,且f(2)=0,从而得到$lo{g}_{b}a=2,a={{b}^{2}}_{\;}$,由此能确定a-a和b-2b的大小关系.
解答 解:设x=logba,由a>b>1,得x>1,
∵(logab)2+${2}^{lo{g}_{b}a}$=$\frac{17}{4}$,且a>b>1,
∴$\frac{1}{{x}^{2}}+{2}^{x}=\frac{17}{4}$,
令f(x)=${2}^{x}+\frac{1}{{x}^{2}}-\frac{17}{4}$,则f(2)=0,
∴$lo{g}_{b}a=2,a={{b}^{2}}_{\;}$,
${a}^{-a}=({b}^{2})^{-{b}^{2}}={b}^{-2{b}^{2}}$,
∵b>1,∴-2b2<-2b,
∴a-a<b-2b.
点评 本题考查两个数的大小的比较,是中档题,解题时要认真审题,注意换元法、构造法和导数性质的合理运用.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
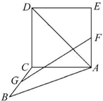 如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为$\frac{\sqrt{3}}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com