
| A. | (3,-3) | B. | $(-\sqrt{3},3)$ | C. | $(\sqrt{3},-3)$ | D. | $(3,-\sqrt{3})$ |
分析 设A(x1,y1),B(x2,y2),弦AB的中点M(x0,y0).由直线参数方程消去参数t化为:$\sqrt{3}$x-y-4$\sqrt{3}$=0.与圆的方程联立化为:4x2-24x+48-R2=0,由已知可得:△>0.利用根与系数的关系、中点坐标公式即可得出.
解答 解:设A(x1,y1),B(x2,y2),弦AB的中点M(x0,y0).
由直线$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=-3\sqrt{3}+\frac{{\sqrt{3}}}{2}t\end{array}\right.$(t为参数)消去参数化为:$\sqrt{3}$x-y-4$\sqrt{3}$=0.
联立$\left\{\begin{array}{l}{\sqrt{3}x-y-4\sqrt{3}=0}\\{{x}^{2}+{y}^{2}={R}^{2}}\end{array}\right.$,化为:4x2-24x+48-R2=0,
由已知可得:△>0.
∴x1+x2=6,
∴x0=$\frac{{x}_{1}+{x}_{2}}{2}$=3,y0=$\sqrt{3}×3-4\sqrt{3}$=-$\sqrt{3}$,
可得M$(3,-\sqrt{3})$.
故选:D.
点评 本题考查了直线的参数方程化为普通方程、直线与圆相交问题、中点坐标公式、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于中档题.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
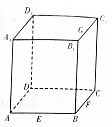 已知点E、F、G分别为正方体ABCD-A1B1C1D1的棱AB、BC、$B_1^{\;}{C_1}$的中点,如图,则下列命题为假命题的是( )
已知点E、F、G分别为正方体ABCD-A1B1C1D1的棱AB、BC、$B_1^{\;}{C_1}$的中点,如图,则下列命题为假命题的是( )| A. | 点P在直线FG上一定,总有AP⊥DE | |
| B. | 点Q在直线BC1上运动时,三棱锥A-D1QC的体积为定值 | |
| C. | 点M是正方体面A1B1C1D1内的点到点D和点C1距离相等的点,则M的轨迹是一条直线 | |
| D. | 过F,D1,G的截面是正方形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ex1-ex2<lnx1-lnx2 | B. | ex1-ex2>lnx1-lnx2 | ||
| C. | x1ex2<x2ex1 | D. | x1ex2>x2ex1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cosx+2 | B. | -cosx-2 | C. | cosx-2 | D. | -cosx+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | -$\frac{{\sqrt{3}}}{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{1}{3}$ | C. | -1 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com