
分析 问题转化为y=-m和g(x)=${(\frac{1}{2})}^{|x-1|}$(x>0),的交点个数,画出函数g(x)的图象,从而求出m的范围即可.
解答 解:f(x)是奇函数,f(x)有5个零点,
x=0是1个,只需x>0时有2个零点即可,
当x>0时,f(x)=($\frac{1}{2}}$)|x-1|+m,
问题转化为y=-m和g(x)=${(\frac{1}{2})}^{|x-1|}$(x>0),的交点个数即可,
函数画出g(x)的图象,如图示: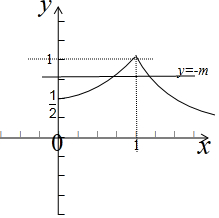 ,
,
结合图象只需$\frac{1}{2}$<-m<1,
即-1<m<-$\frac{1}{2}$,
故答案为:$({-1,-\frac{1}{2}})$.
点评 本题考查了函数的零点问题,考查数形结合思想以及转化思想,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | (3,-3) | B. | $(-\sqrt{3},3)$ | C. | $(\sqrt{3},-3)$ | D. | $(3,-\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
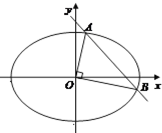 已知焦点在x轴上的椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),焦距为2$\sqrt{3}$,长轴长为4.直线l与椭圆交于A,B两点,O为坐标原点,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,
已知焦点在x轴上的椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),焦距为2$\sqrt{3}$,长轴长为4.直线l与椭圆交于A,B两点,O为坐标原点,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\frac{1}{x}$ | B. | y=3-x | C. | y=|x| | D. | y=-x2+4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com