
如图,平面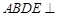 平面
平面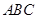 ,
,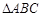 是等腰直角三角形,
是等腰直角三角形,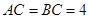 ,四边形
,四边形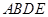 是直角梯形,
是直角梯形,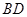 ∥AE,
∥AE,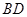
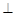
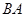 ,
,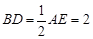 ,
,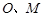 分别为
分别为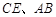 的中点.
的中点.
(1)求异面直线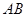 与
与 所成角的大小;
所成角的大小;
(2)求直线 和平面
和平面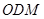 所成角的正弦值.
所成角的正弦值.
(1)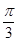 ,(2)
,(2)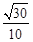
解析试题分析:(1)求空间角,一般利用空间向量解决.首先要建立恰当的空间直角坐标系,由平面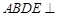 平面
平面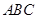 及
及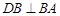 ,运用面面垂直性质定理,可得
,运用面面垂直性质定理,可得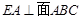 ,这样确定竖坐标.横坐标与纵坐标可根据右手系建立.因为异面直线
,这样确定竖坐标.横坐标与纵坐标可根据右手系建立.因为异面直线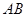 与
与 所成角
所成角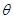 等于向量
等于向量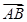 与
与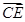 夹角或其补角,而异面直线
夹角或其补角,而异面直线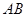 与
与 所成角范围为
所成角范围为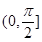 ,所以
,所以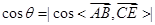 ,(2) 直线
,(2) 直线 和平面
和平面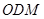 所成角
所成角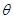 与向量
与向量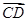 与平面
与平面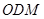 法向量
法向量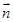 夹角互余或相差
夹角互余或相差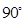 ,而直线
,而直线 和平面
和平面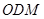 所成角
所成角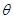 范围为
范围为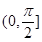 ,所以
,所以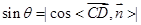 .
.
试题解析:
∵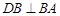 ,又∵面
,又∵面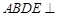 面
面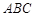 ,面
,面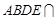 面
面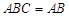 ,
, ,∴
,∴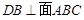 ,∵BD∥AE,∴
,∵BD∥AE,∴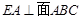 , 2分
, 2分
如图所示,以C为原点,分别以CA,CB为x,y轴,以过点C且与平面ABC垂直的直线为z轴,建立空间直角坐标系,∵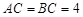 ,∴设各点坐标为
,∴设各点坐标为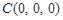 ,
,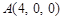 ,
, ,
, ,
,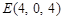 ,
,
则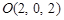 ,
,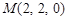 ,
,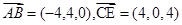 ,
,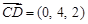 ,
,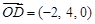 ,
,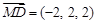 .
.
(1)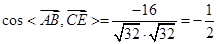 ,
,
则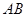 与
与 所成角为
所成角为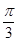 . 5分
. 5分
(2)设平面ODM的法向量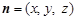 ,则由
,则由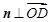 ,且
,且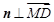 可得
可得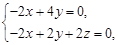
令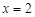 ,则
,则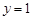 ,
,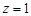 ,∴
,∴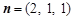 ,设直线CD和平面ODM所成角为
,设直线CD和平面ODM所成角为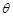 ,则
,则 ,
,
∴直线CD和平面ODM所成角的正弦值为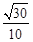 . 10分
. 10分
考点:利用空间向量求异面直线所成角及直线与平面所成角.


科目:高中数学 来源: 题型:解答题
如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F,G分别是AB,AD,CD的中点,计算: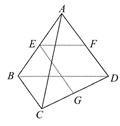
(1) ·
· .
.
(2)EG的长.
(3)异面直线EG与AC所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为CD的中点.
(1)求证:B1E⊥AD1.
(2)在棱AA1上是否存在一点P,使得DP∥平面B1AE?若存在,求AP的长;若不存在,说明理由.
(3)若二面角A-B1E-A1的大小为30°,求AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四边形ABCD为矩形,PD⊥平面ABCD,PD∥QA,QA=AD=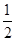 PD.
PD.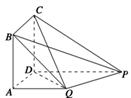
(1)求证:平面PQC⊥平面DCQ;
(2)若二面角Q-BP-C的余弦值为-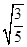 ,求
,求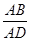 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,四棱锥S ABCD的底面是正方形,每条侧棱的长都是底面边长的
ABCD的底面是正方形,每条侧棱的长都是底面边长的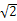 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.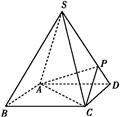
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P AC
AC D的大小;
D的大小;
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SE∶EC的值;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
四棱锥 中,底面
中,底面 为平行四边形,侧面
为平行四边形,侧面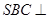 面
面 ,已知
,已知
(Ⅰ)求证: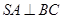 ;
;
(Ⅱ)在SB上选取点P,使SD//平面PAC ,并证明;
(Ⅲ)求直线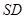 与面
与面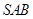 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在棱长为1正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点
(1)求直线AM和CN所成角的余弦值;
(2)若P为B1C1的中点,求直线CN与平面MNP所成角的余弦值;
(3)P为B1C1上一点,且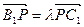 ,当 B1D⊥面PMN时,求
,当 B1D⊥面PMN时,求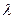 的值.
的值.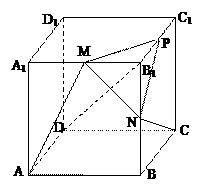
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com