
【题目】已知函数f(x)=(log2x﹣2)(log4x﹣ ![]() )
)
(1)当x∈[2,4]时,求该函数的值域;
(2)若f(x)>mlog2x对于x∈[4,16]恒成立,求m的取值范围.
【答案】
(1)解:f(x)=(log2x﹣2)(log4x﹣ ![]() )
)
= ![]() (log2x)2﹣
(log2x)2﹣ ![]() log2x+1,2≤x≤4
log2x+1,2≤x≤4
令t=log2x,则y= ![]() t2﹣
t2﹣ ![]() t+1=
t+1= ![]() (t﹣
(t﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∵2≤x≤4,
∴1≤t≤2.
当t= ![]() 时,ymin=﹣
时,ymin=﹣ ![]() ,当t=1,或t=2时,ymax=0.
,当t=1,或t=2时,ymax=0.
∴函数的值域是[﹣ ![]() ,0]
,0]
(2)解:令t=log2x,得 ![]() t2﹣
t2﹣ ![]() t+1>mt对于2≤t≤4恒成立.
t+1>mt对于2≤t≤4恒成立.
∴m< ![]() t+
t+ ![]() ﹣
﹣ ![]() 对于t∈[2,4]恒成立,
对于t∈[2,4]恒成立,
设g(t)= ![]() t+
t+ ![]() ﹣
﹣ ![]() ,t∈[2,4],
,t∈[2,4],
∴g(t)= ![]() t+
t+ ![]() ﹣
﹣ ![]() =
= ![]() (t+
(t+ ![]() )﹣
)﹣ ![]() ,
,
∵g(t)= ![]() t+
t+ ![]() ﹣
﹣ ![]() 在[2,4]上为增函数,
在[2,4]上为增函数,
∴当t=2时,g(t)min=g(2)=0,
∴m<0.
【解析】(1)f(x)=(log2x﹣2)(log4x﹣ ![]() )=
)= ![]() (log2x)2﹣
(log2x)2﹣ ![]() log2x+1,2≤x≤4,令t=log2x,则y=
log2x+1,2≤x≤4,令t=log2x,则y= ![]() t2﹣
t2﹣ ![]() t+1=
t+1= ![]() (t﹣
(t﹣ ![]() )2﹣
)2﹣ ![]() ,由此能求出函数的值域.(2)令t=log2x,得
,由此能求出函数的值域.(2)令t=log2x,得 ![]() t2﹣
t2﹣ ![]() t+1>mt对于2≤t≤4恒成立,从而得到m<
t+1>mt对于2≤t≤4恒成立,从而得到m< ![]() t+
t+ ![]() ﹣
﹣ ![]() 对于t∈[2,4]恒成立,构造函数g(t)=
对于t∈[2,4]恒成立,构造函数g(t)= ![]() t+
t+ ![]() ﹣
﹣ ![]() ,t∈[2,4],能求出m的取值范围.
,t∈[2,4],能求出m的取值范围.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求实数![]() 、
、![]() 的值;
的值;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(Ⅲ)曲线![]() 上存在两点
上存在两点![]() 、
、![]() ,使得
,使得![]() 是以坐标原点
是以坐标原点![]() 为直角顶点的直角三角形,且斜边
为直角顶点的直角三角形,且斜边![]() 的中点在
的中点在![]() 轴上,求实数
轴上,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左右焦点分别为
,左右焦点分别为![]() 是椭圆在第一象限上的一个动点,圆
是椭圆在第一象限上的一个动点,圆![]() 与
与![]() 的延长线,
的延长线, ![]() 的延长线以及线段
的延长线以及线段![]() 都相切,
都相切, ![]() 为一个切点.
为一个切点.
(1)求椭圆方程;
(2)设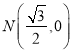 ,过
,过![]() 且不垂直于坐标轴的动点直线
且不垂直于坐标轴的动点直线![]() 交椭圆于
交椭圆于![]() 两点,若以
两点,若以![]() 为邻边的平行四边形是菱形,求直线
为邻边的平行四边形是菱形,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以坐标原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点![]() 的极坐标为
的极坐标为![]() ,圆
,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),(1)直线
为参数),(1)直线![]() 过
过![]() 且与圆
且与圆![]() 相切,求直线
相切,求直线![]() 的极坐标方程;(2)过点
的极坐标方程;(2)过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2+ax﹣6a2≤0},B={x||x﹣2|<a},
(1)当a=1时,求A∩B和A∪B;
(2)当BA时,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(2ax+1)+ ![]() ﹣x2﹣2ax(a∈R).
﹣x2﹣2ax(a∈R).
(1)若x=2为f(x)的极值点,求实数a的值;
(2)若y=f(x)在[3,+∞)上为增函数,求实数a的取值范围;
(3)当a=﹣ ![]() 时,方程f(1﹣x)=
时,方程f(1﹣x)= ![]() 有实根,求实数b的最大值.
有实根,求实数b的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+alnx.
(1)当a=1时,求曲线f(x)在点(1,f(1))处的切线方程;
(2)当a=﹣2时,求函数f(x)的极值;
(3)若函数g(x)=f(x)+ ![]() 在[1,4]上是减函数,求实数a的取值范围.
在[1,4]上是减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:参数方程与极坐标系
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() 为倾斜角),以坐标原点O为极点,
为倾斜角),以坐标原点O为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的直角坐标方程,并 求C的焦点F的直角坐标;
的直角坐标方程,并 求C的焦点F的直角坐标;
(2)已知点![]() ,若直线
,若直线![]() 与C相交于A,B两点,且
与C相交于A,B两点,且![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com