
| A. | 2π-4 | B. | π-4 | C. | ln2-4 | D. | ln2-2 |
分析 根据定积分的运算,$\int_0^2{({\sqrt{4-{x^2}}-2x})dx=}$${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx+${∫}_{0}^{2}$(-2x)dx,根据定积分的运算及定积分的几何意义,即可求得答案.
解答 解:$\int_0^2{({\sqrt{4-{x^2}}-2x})dx=}$${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx+${∫}_{0}^{2}$(-2x)dx,
由${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx的几何意义表示以原点为圆心,以2为半径的圆面积的$\frac{1}{4}$,
∴${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx=$\frac{1}{4}$×πr2=π,
${∫}_{0}^{2}$(-2x)dx=-x2${丨}_{0}^{2}$=-4,
∴$\int_0^2{({\sqrt{4-{x^2}}-2x})dx=}$${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx+${∫}_{0}^{2}$(-2x)dx=π-4,
∴$\int_0^2{({\sqrt{4-{x^2}}-2x})dx=}$π-4,
故选B.
点评 本题考查定积分的运算,考查定积分的几何意义,考查计算能力,属于中档题.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:填空题
 如图,点A的坐标为(1,0),函数y=ax2过点C(2,4),若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于$\frac{5}{12}$.
如图,点A的坐标为(1,0),函数y=ax2过点C(2,4),若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于$\frac{5}{12}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3]∪[4,+∞) | B. | [-3,4] | C. | (-∞,-2]∪[5,+∞) | D. | [-2,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
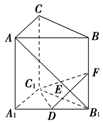 直三棱柱ABC-A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E,要使AB1⊥平面C1DF,则线段B1F的长为( )
直三棱柱ABC-A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E,要使AB1⊥平面C1DF,则线段B1F的长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com