
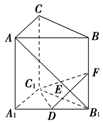
 直三棱柱ABC-A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E,要使AB1⊥平面C1DF,则线段B1F的长为( )
直三棱柱ABC-A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E,要使AB1⊥平面C1DF,则线段B1F的长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
分析 作DE⊥AB1交AB1于E,延长DE交BB1于F,连接C1F,则AB1⊥平面C1DF,点FB1B的中点即为所求,由C1D⊥平面AA1BB,AB1?平面AA1B1B,则C1D⊥AB1,AB1⊥DF,DF∩C1D=D,满足线面垂直的判定定理,则AB1⊥平面C1DF
解答 解:作DE⊥AB1交AB1于E,延长DE交BB1于F,连接C1F,则AB1⊥平面C1DF,点F即为所求.
∵C1D⊥平面AA1B1B,AB1?平面AA1B1B,
∴C1D⊥AB1.又AB1⊥DF,DF∩C1D=D,
∴AB1⊥平面C1DF.
四边形AA1B1B为正方形,此时点F为B1B的中点.
如图则有△AA1B1∽DB1F,即$\frac{A{A}_{1}}{D{B}_{1}}=\frac{{A}_{1}B}{{B}_{1}F}$⇒${B}_{1}F=\frac{1}{2}$.
故选:A
点评 本题主要考查了直线与平面垂直的判定.应熟练记忆直线与平面垂直的判定定理,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
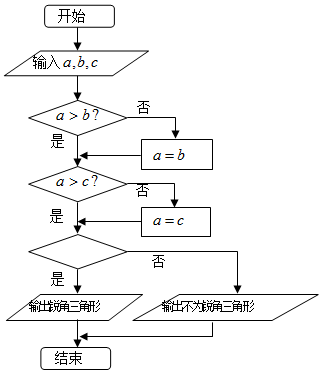 下面程序框图中,若输入互不相等的三个正实数a,b,c(abc≠0),要求判断△ABC的形状,则空白的判断框应填入( )
下面程序框图中,若输入互不相等的三个正实数a,b,c(abc≠0),要求判断△ABC的形状,则空白的判断框应填入( )| A. | a2+b2>c2? | B. | a2+c2>b2? | C. | b2+c2>a2? | D. | b2+a2=c2? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 18 | C. | 21 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\overrightarrow{EF}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{CD}$ | B. | $\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{AB}$$+\frac{1}{3}$$\overrightarrow{CD}$ | C. | $\overrightarrow{EF}$=$\overrightarrow{AB}$+$\overrightarrow{CD}$ | D. | $\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{AB}$$+\frac{2}{3}$$\overrightarrow{CD}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com