
分析 (1)将两女生看作一个元素,使用捆绑法排列;
(2)插空法排列;
(3)相除法计算;
(4)分类法计算.
解答 解:(1)两名女生站在一起有站法A${\;}_{2}^{2}$种,视为一种元素与其余5人全排,有A${\;}_{6}^{6}$种排法.
故有不同站法A${\;}_{2}^{2}$•A${\;}_{6}^{6}$=1 440种.
(2)先站老师和女生,有站法A${\;}_{3}^{3}$种,再在老师和女生站位的间隔(含两端)处插入男生,每空一人,有插入方法A${\;}_{4}^{4}$种.
故共A${\;}_{3}^{3}$•A${\;}_{4}^{4}$=144种.
(3)7人全排列中,4名男生不考虑身高顺序的站法有A${\;}_{4}^{4}$种,而由高到低有从左到右,或从右到左的不同.
故共有不同站法2•$\frac{{A}_{7}^{7}}{{A}_{4}^{4}}$=420种.
(4)中间和两端是特殊位置,可如下分类求解:
①老师站两端之一,另一端由男生站,有A${\;}_{2}^{1}$•A${\;}_{4}^{1}$•A${\;}_{5}^{5}$种站法,
②两端全由男生站,老师站除两端和正中间的另外4个位置之一,有A${\;}_{4}^{2}$•A${\;}_{4}^{1}$•A${\;}_{4}^{4}$种站法.
故共有不同站法有A${\;}_{2}^{1}$•A${\;}_{4}^{1}$•A${\;}_{5}^{5}$+A${\;}_{4}^{2}$•A${\;}_{4}^{1}$•A${\;}_{4}^{4}$=2 112种.
点评 本题考查了计数原理,排列与排列数的计算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\overrightarrow{EF}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{CD}$ | B. | $\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{AB}$$+\frac{1}{3}$$\overrightarrow{CD}$ | C. | $\overrightarrow{EF}$=$\overrightarrow{AB}$+$\overrightarrow{CD}$ | D. | $\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{AB}$$+\frac{2}{3}$$\overrightarrow{CD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | af(b)>bf(a) | B. | bf(a)>af(b) | C. | af(a)<bf(b) | D. | af(a)>bf(b) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
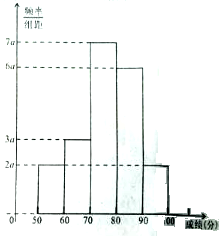 20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com