
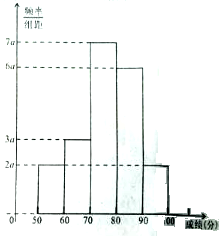
 20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.分析 (1)根据频率分布直方图求出a的值;
(2)由图可知,成绩在[50,60)和[60,70)的频率分别为0.1和0.15,用样本容量20乘以对应的频率,即得对应区间内的人数,从而求出所求.
(3)分别列出满足[50,70)的基本事件,再找到在[60,70)的事件个数,根据古典概率公式计算即可.
解答 解:(1)根据直方图知组距=10,由(2a+3a+6a+7a+2a)×10=1,解得a=0.005.
(2)成绩落在[50,60)中的学生人数为2×0.005×10×20=2,
成绩落在[60,70)中的学生人数为3×0.005×10×20=3.
(3)记成绩落在[50,60)中的2人为A,B,成绩落在[60,70)中的3人为C,D,E,
则成绩在[50,70)的学生任选2人的基本事件有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共10个,
其中2人的成绩都在[60,70)中的基本事件有CD,CE,DE共3个,
故所求概率为P=$\frac{3}{10}$.
点评 本题考查频率分布直方图的应用以及古典概型的概率的应用,属于中档题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,+∞) | B. | (-2,+∞) | C. | (-2,0)∪(0,+∞) | D. | [-2,0)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com