
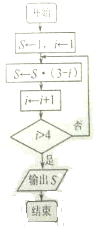
 阅读如图所示的程序框图,运行相应的程序,则输出S的值是0.
阅读如图所示的程序框图,运行相应的程序,则输出S的值是0. 科目:高中数学 来源: 题型:选择题
| A. | af(b)>bf(a) | B. | bf(a)>af(b) | C. | af(a)<bf(b) | D. | af(a)>bf(b) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
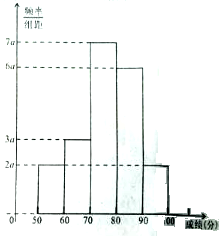 20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
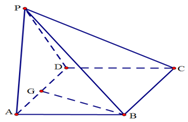 如图,四棱锥P-ABCD中,底面ABCD是∠DAB且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD是∠DAB且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 甲、乙、丙.丁四辆玩具赛车同时从起点出发并做匀速直线运动,丙车最先到达终点.丁车最后到达终点.若甲、乙两车的s-t图象如图所示,则对于丙、丁两车的图象所在区域,判断正确的是( )
甲、乙、丙.丁四辆玩具赛车同时从起点出发并做匀速直线运动,丙车最先到达终点.丁车最后到达终点.若甲、乙两车的s-t图象如图所示,则对于丙、丁两车的图象所在区域,判断正确的是( )| A. | 丙在Ⅲ区域,丁在Ⅰ区域 | B. | 丙在Ⅰ区城,丁在Ⅲ区域 | ||
| C. | 丙在Ⅱ区域,丁在Ⅰ区域 | D. | 丙在Ⅲ区域,丁在Ⅱ区域 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com