
分析 (1)集合M表示的区域的面积为6×4=24,此圆x2+y2=4的面积表示满足条件的基本事件,所求为面积比;
(2)求出满足以(x,y)为坐标的点到直线x+y=0的距离不大于$\sqrt{2}$面积,则求面积比即可.
解答  解:(1)A=[-3,3],B=[-2,2],设M={(x,y)|x∈A,y∈B},表示的区域的面积为6×4=24.
解:(1)A=[-3,3],B=[-2,2],设M={(x,y)|x∈A,y∈B},表示的区域的面积为6×4=24.
圆x2+y2=4的面积为4π,
∴以(x,y)为坐标的点落在圆x2+y2=4内的概率为P1=$\frac{4π}{24}$=$\frac{π}{6}$,
(2)由题意,到直线x+y=0的距离不大于$\sqrt{2}$的点为夹在两条平行直线x+y-2=0与x+y+2=0之间的范围内,如图所示,
故所求事件的概率为${P_2}=\frac{{6×4-2×\frac{1}{2}×3×3}}{6×4}=\frac{5}{8}$.
点评 本题考查了几何概型的概率求法,关键是将所求的概率利用基本事件的集合度量即区域的长度或者面积或者体积表示,求比值.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
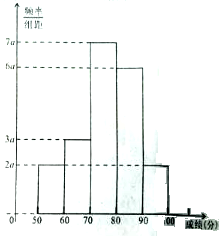 20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 甲、乙、丙.丁四辆玩具赛车同时从起点出发并做匀速直线运动,丙车最先到达终点.丁车最后到达终点.若甲、乙两车的s-t图象如图所示,则对于丙、丁两车的图象所在区域,判断正确的是( )
甲、乙、丙.丁四辆玩具赛车同时从起点出发并做匀速直线运动,丙车最先到达终点.丁车最后到达终点.若甲、乙两车的s-t图象如图所示,则对于丙、丁两车的图象所在区域,判断正确的是( )| A. | 丙在Ⅲ区域,丁在Ⅰ区域 | B. | 丙在Ⅰ区城,丁在Ⅲ区域 | ||
| C. | 丙在Ⅱ区域,丁在Ⅰ区域 | D. | 丙在Ⅲ区域,丁在Ⅱ区域 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
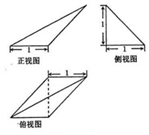
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com