
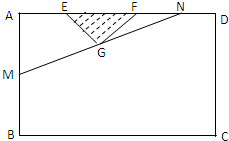
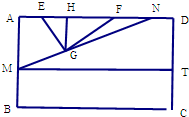
 某小区想利用一矩形空地ABCD建造市民健身广场,设计时决定保留空地边上的一个水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且△EFG中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一条直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场.
某小区想利用一矩形空地ABCD建造市民健身广场,设计时决定保留空地边上的一个水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且△EFG中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一条直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场.| 1 |
| 2 |
| 5(60-x)2 |
| 40-x |
| NH |
| HG |
| NA |
| AM |
| 40-x |
| 10 |
| 60-x |
| AM |
| 600-10x |
| 40-x |
| 1 |
| 2 |
| 600-10x |
| 40-x |
| 1 |
| 2 |
| (x+60)(600-10x) |
| 40-x |
| 5(60-x)2 |
| 40-x |
| 5(60-x)2 |
| 40-x |
| 400 |
| 40-x |
| 400 |
| 40-x |


科目:高中数学 来源: 题型:
 (理科) 为了近似求出圆周率的值,有人设计如下方法来进行随机模拟:如图,双曲线
(理科) 为了近似求出圆周率的值,有人设计如下方法来进行随机模拟:如图,双曲线| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4 |
| 5 |
| A+B |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
. |
| x |
. |
| y |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| A、(∁RM)∩N=∅ |
| B、M∪N=R |
| C、M?N |
| D、(∁RM)∪N=R |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com