
【题目】如图所示,圆锥的底面![]() 半径为2,
半径为2,![]() 是圆周上的定点,动点
是圆周上的定点,动点![]() 在圆周上逆时针旋转,设
在圆周上逆时针旋转,设![]() (
(![]() ),
),![]() 是母线
是母线![]() 的中点,已知当
的中点,已知当![]() 时,
时,![]() 与底面所成角为
与底面所成角为![]() .
.
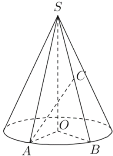
(1)求该圆锥的侧面积;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() .(2)
.(2)![]() 或
或![]() .
.
【解析】
(1)作出![]() 与底面所成角
与底面所成角![]() ,利用
,利用![]() ,由此求得
,由此求得![]() ,进而求得圆锥的侧面积.
,进而求得圆锥的侧面积.
(2)解法一:建立空间直角坐标系,利用![]() 求得
求得![]() 的值,进而求得
的值,进而求得![]() 的值.
的值.
解法二:判断出三角形![]() 是等边三角形,由此求得
是等边三角形,由此求得![]() 的值.
的值.
解法三:通过构造直角三角形的方法,求得![]() 的值,进而求得
的值,进而求得![]() 的值.
的值.
(1)![]() ,
,![]() ,
,
设![]() 为
为![]() 中点,连接
中点,连接![]() ,则
,则![]() ∥
∥![]() ,
,
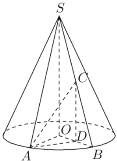
∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]()
在Rt△![]() 中,
中,![]() ,
,![]() ,得:
,得:![]() ,
,
得:![]() ,
,![]() ,
,
∴![]() ,
,
![]() .
.
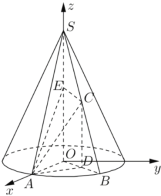
(2)解法一:如图建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
由题意,![]() ,
,
∵![]() ,∴
,∴![]() 或
或![]() .
.
解法二:设![]() 为
为![]() 中点,连接
中点,连接![]() ,则
,则![]() ∥
∥![]() , ∴
, ∴![]() ,
,
又∵![]() ,可得:
,可得:![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴△![]() 是等边三角形,
是等边三角形,
∴![]() 或
或![]() .
.
解法三:设![]() 为
为![]() 中点,连接
中点,连接![]()
![]() ,∴
,∴![]()
设![]() 为
为![]() 中点,连接
中点,连接![]()
![]() ,∴
,∴![]() ,
,
在△![]() 中,由余弦定理有:
中,由余弦定理有:![]() ,
,
∴在Rt△![]() 中,
中,![]() ,在△
,在△![]() 中,
中,![]() ,
,
∴在Rt△![]() 中,
中,![]() ,即得
,即得![]() ,
,
∵![]() ,∴
,∴![]() 或
或![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() 与圆
与圆![]() 相外切,且与直线
相外切,且与直线![]() 相切.
相切.
(1)记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,求
,求![]() 的方程;
的方程;
(2)过点![]() 的两条直线
的两条直线![]() 与曲线
与曲线![]() 分别相交于点
分别相交于点![]() 和
和![]() ,线段
,线段![]() 和
和![]() 的中点分别为
的中点分别为![]() .如果直线
.如果直线![]() 与
与![]() 的斜率之积等于1,求证:直线
的斜率之积等于1,求证:直线![]() 经过定点.
经过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为坐标原点,动点
为坐标原点,动点![]() 在圆
在圆![]() 上,过
上,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 上的点
上的点![]() 满足
满足![]() .过点
.过点![]() 作直线
作直线![]() 垂直于线段
垂直于线段![]() 交
交![]() 于点
于点![]() .
.
(ⅰ)证明:![]() 恒过定点;
恒过定点;
(ⅱ)设线段![]() 交
交![]() 于点
于点![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为助力湖北新冠疫情后的经济复苏,某电商平台为某工厂的产品开设直播带货专场.为了对该产品进行合理定价,用不同的单价在平台试销,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)根据以上数据,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该产品成本是4元/件,假设该产品全部卖出,预测把单价定为多少时,工厂获得最大利润?
(参考公式:回归方程![]() ,其中
,其中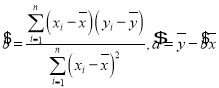 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为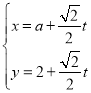 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 坐标为
坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为平行四边形,
为平行四边形,![]() ,且
,且![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.
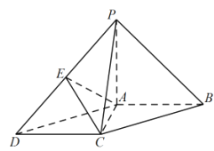
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在线段![]() 上(不含端点)是否存在一点
上(不含端点)是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,确定
?若存在,确定![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下三个条件:
①数列![]() 是首项为 2,满足
是首项为 2,满足![]() 的数列;
的数列;
②数列![]() 是首项为2,满足
是首项为2,满足![]() (λ∈R)的数列;
(λ∈R)的数列;
③数列![]() 是首项为2,满足
是首项为2,满足![]() 的数列..
的数列..
请从这三个条件中任选一个将下面的题目补充完整,并求解.
设数列![]() 的前n项和为
的前n项和为![]() ,
,![]() 与
与![]() 满足______,记数列
满足______,记数列![]() ,
,![]() ,求数列{
,求数列{![]() }的前n项和
}的前n项和![]() ;
;
(注:如选择多个条件分别解答,按第一个解答计分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com