练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    小明手中有5张扑克牌，其中2张为不同花色的k，3张为不同花色的A．规定每次只能出同一种点数的牌（可以只出一张，也可出多张），出牌后不再后收回，且同一次所出的牌不考虑顺序，若小明恰好4次把牌出完，则他不同的出牌方式种数共有（　　）
    A、48B、74C、96D、98
    考点：计数原理的应用
    专题：排列组合
    分析：根据题意，5张扑克牌恰好4次把牌出完，则必须有一次出2张同一种点数的牌，先确定这两张，当这两张2张为不同花色的k时和当这两张2张为不同花色的A时，分别计算每种情况的出牌方法数目，由分类计数原理计算可得答案．
    解答： 解：根据题意，5张扑克牌恰好4次把牌出完，则必须有一次出2张同一种点数的牌，先确定这两张，
    分两类，当这两张2张为不同花色的k时，有
    A
    4
    4
    =24种，
    当这两张2张为不同花色的A时，有
    C
    2
    3
    •
    A
    4
    4
    =72种，
    根据分类计数原理，则他不同的出牌方式种数共有24+72=96种
    故选：C
    点评：本题考查排列、组合的应用，解题的关键在于全面考虑，按一定顺序分类讨论、计算，做到不重不漏，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知实数x、y满足4x2+y2-xy=1，且不等式2x+y+c＞0恒成立，则c的取值范围是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    “a=1”是“直线l1：ax+y-1=0与直线l2：4x+（a+3）y+5+a=0平行”的（　　）
    A、充分而不必要条件
    B、必要而不充分条件
    C、充要条件
    D、既不充分又不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，已知下列条件，解三角形．
    （1）A=
    π
    6
    ，a=25，b=50
    		2
    ；
    （2）A=
    π
    6
    ，a=
    50
    		6
    3
    ，b=50
    		2
    ；
    （3）A=
    π
    6
    ，a=50，b=50
    		2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知锐角△ABC中，∠B=
    π
    4
    ，b=5，sinA=
    2
    		2
    3
    ．求S△ABC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

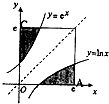    如图，在边长为e（e为自然对数的底数）的正方形区域的A处于C处各有一个通信基站，其信号覆盖范围分别为如图所示的阴影区域．该正方形区域内无其它信号来源且这两个基站工作正常，若在该正方形区域内随机选择一个地点，则该地点无信号的概率为（　　）
    A、
    2
    e2
    B、1-
    2
    e2
    C、
    1
    e
    D、1-
    1
    e

    查看答案和解析>>

    科目：高中数学 来源： 题型：

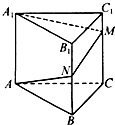    已知三棱柱AB-A1B1C1的侧棱垂直于底面，且底面边长与侧棱长都等于3，蚂蚁从A点沿侧面经过棱BB1上的点N和CC1上的点M爬到点A1，如图所示，则当蚂蚁爬过的路程最短时，直线MN与平面ABC所成角的正弦值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    关于函数f（x）=x2（lnx-a）+a，给出以下4个结论：
    ①?a＞0，?x＞0，f（x）≥0；
    ②?a＞0，?x＞0，f（x）≤0；
    ③?a＞0，?x＞0，f（x）≥0；
    ④?a＞0，?x＞0，f（x）≤0．
    其中正确结论的个数是（　　）
    A、0B、1C、2D、3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知等差数列{an}的公差为d（d＞0），a1=1，S5=35，则d的值为（　　）
    A、3B、-3C、2D、4

    查看答案和解析>>

    同步练习册答案