
分析 (Ⅰ)根据极坐标和普通坐标之间的关系进行转化求解即可.
(Ⅱ)设出直线PQ的参数方程,利用参数的几何意义进行求解即可.
解答 解:( I)C1的直角坐标方程为(x-1)2+y2=1,…(2分),
C2的直角坐标方程为x=3;…(4分)
( II)设曲线C1与x轴异于原点的交点为A,
∴PQ过点A(2,0),
设直线PQ的参数方程为:$\left\{\begin{array}{l}{x=2+tcosθ}\\{y=tsinθ}\end{array}\right.$,
代入C1可得t2+2tcosθ=0,解得,
可知|AP|=|t2|=|2cosθ|…(6分)
代入C2可得2+tcosθ=3,解得${t^/}=\frac{1}{cosθ}$,
可知$|AQ|=|{t^/}|=|\frac{1}{cosθ}|$ …(8分)
所以PQ=$|AP|+|AQ|=|2cosθ|+|\frac{1}{cosθ}|≥2\sqrt{2}$,当且仅当$|2cosθ|=|\frac{1}{cosθ}|$时取等号,
所以线段PQ长度的最小值为$2\sqrt{2}$.…(10分)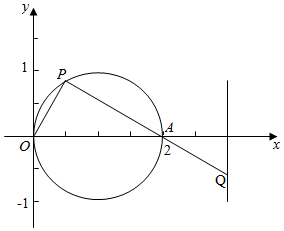
点评 本题主要考查极坐标方程和普通坐标方程之间的转化,考查学生的转化能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,⊙O1与⊙O2外切于点P,从⊙O1上点A作的切线AB,切点为B,连AP(不过O1)并延长与⊙O2交于点C.
如图所示,⊙O1与⊙O2外切于点P,从⊙O1上点A作的切线AB,切点为B,连AP(不过O1)并延长与⊙O2交于点C.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
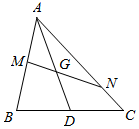 如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB、AC于M、N两点.若$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则$\frac{1}{x}$+$\frac{1}{y}$=4.
如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB、AC于M、N两点.若$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则$\frac{1}{x}$+$\frac{1}{y}$=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
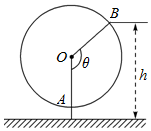 (1,3班做)一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面间的距离为h.
(1,3班做)一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面间的距离为h.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com