
���� ������ɵ�f��x��=2sin��2x+$\frac{��}{3}$��������С�����ڣ��ⲻ��ʽ2k��-$\frac{��}{2}$��2x+$\frac{��}{3}$2k��+$\frac{��}{2}$�ɵú����ĵ����������䣻
������������A=$\frac{��}{3}$�������Ҷ����ɵ�b+c=13�������Ҷ����ɵ�bc=40�����������ʽS=$\frac{1}{2}$bcsinA����ɵã�
��� �⣺����f��x��=2sinxcosx+2$\sqrt{3}$cos2x-$\sqrt{3}$=sin2x+$\sqrt{3}$cos2x=2sin��2x+$\frac{��}{3}$������2�֣�
��y=f��x������С������ΪT=�С���3�֣�
��2k��-$\frac{��}{2}$��2x+$\frac{��}{3}$2k��+$\frac{��}{2}$�ɵ�k��-$\frac{5��}{12}$��x��k��+$\frac{��}{12}$��
�ຯ���ĵ�����������Ϊ[k��-$\frac{5��}{12}$��k��+$\frac{��}{12}$]��k��Z��������6�֣�
����f��$\frac{A}{2}$-$\frac{��}{6}$��=$\sqrt{3}$����2sinA=$\sqrt{3}$��
��0��A��$\frac{��}{2}$����A=$\frac{��}{3}$������7�֣�
�����Ҷ����ã�sinB+sinC=$\frac{{13\sqrt{3}}}{14}$=$\frac{b+c}{7}��\frac{\sqrt{3}}{2}$
��b+c=13����9�֣�
�����Ҷ���a2=b2+c2-2bccosA=��b+c��2-2bc-2bccosA��
�������ݿɵ�49=169-3bc����bc=40����11�֣�
���ABC�����S=$\frac{1}{2}$bcsinA=$\frac{1}{2}��40��\frac{\sqrt{3}}{2}$=10$\sqrt{3}$����12�֣�
���� ���⿼�����Ǻ��������Ǻ�����ʽ���漰���Ǻ����ĵ����Ժ��������Լ��������Σ����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2015}{2016}$ | B�� | $\frac{2015}{1008}$ | C�� | $\frac{2016}{2017}$ | D�� | $\frac{4032}{2017}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
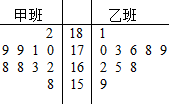 �����ȡij��ѧ�ס��������10��ͬѧ���������ǵ����ߣ���λ��cm��������������ݵľ�Ҷͼ����ͼ��ʾ������ҵ���λ���ֱ�Ϊ��������
�����ȡij��ѧ�ס��������10��ͬѧ���������ǵ����ߣ���λ��cm��������������ݵľ�Ҷͼ����ͼ��ʾ������ҵ���λ���ֱ�Ϊ��������| A�� | 17��17 | B�� | 17��17.3 | C�� | 16.8��17 | D�� | 169��171.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����2 | B�� | �����2 | C�� | �����2 | D�� | ��a��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| һ������ÿ��������x | 5 | 8 | 6 | 4 | 7 |
| ��ѧ�¿��ɼ�y | 82 | 87 | 84 | 81 | 86 |
| A�� | 8 | B�� | 9 | C�� | 10 | D�� | 11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �۽������� | B�� | ֱ�������� | C�� | ��������� | D�� | �ȱ������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com