
| A、1 | B、2 | C、3 | D、4 |


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源:2015届四川省绵阳市高三一诊测试理科数学试卷(解析版) 题型:选择题
已知x∈[-π,π],则“x∈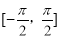 ”是“sin(sinx)<cos(cosx)成立”的( )
”是“sin(sinx)<cos(cosx)成立”的( )
(A)充要条件 (B)必要不充分条件
(C)充分不必要条件 (D)既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届四川省泸州市高三上学期第一次诊断性考试理科数学试卷(解析版) 题型:选择题
学校餐厅每天供应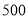 名学生用餐,每星期一有
名学生用餐,每星期一有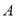 、
、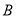 两种菜可供选择。调查表明,凡是在这星期一选
两种菜可供选择。调查表明,凡是在这星期一选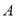 菜的,下星期一会有
菜的,下星期一会有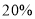 改选
改选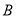 菜;而选
菜;而选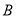 菜的,下星期一会有
菜的,下星期一会有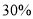 改选
改选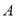 菜。用
菜。用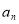 表示第
表示第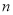 个星期一选
个星期一选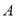 的人数,如果
的人数,如果 ,则
,则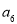 的值为( )
的值为( )
A、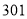 B、
B、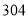 C、
C、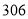 D、
D、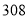
查看答案和解析>>
科目:高中数学 来源:2015届四川省泸州市高三上学期第一次诊断性考试文科数学试卷(解析版) 题型:选择题
设函数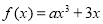 ,其图象在点
,其图象在点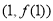 处的切线
处的切线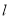 与直线
与直线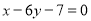 垂直,则直线
垂直,则直线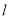 与坐标轴围成的三角形的面积为( )
与坐标轴围成的三角形的面积为( )
A、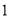 B、
B、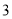 C、
C、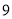 D、
D、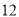
查看答案和解析>>
科目:高中数学 来源:2015届山东省高三第一次诊断性考试理科数学试卷(解析版) 题型:解答题
已知椭圆 ,过焦点垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
,过焦点垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
(1)求椭圆的方程;
(2)过点 的直线l交椭圆于A,B两点,交直线
的直线l交椭圆于A,B两点,交直线 于点E,
于点E, 判断
判断 是否为定值,若是,计算出该定值;不是,说明理由.
是否为定值,若是,计算出该定值;不是,说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届山东师范大学附属中学高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
已知函数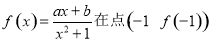 的切线方程为
的切线方程为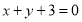 .
.
(1)求函数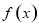 的解析式;
的解析式;
(2)设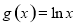 ,求证:
,求证: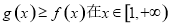 上恒成立;
上恒成立;
(3)已知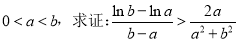 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com