
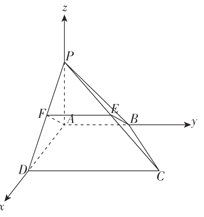
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
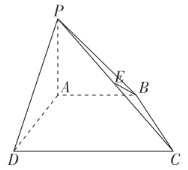
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1) 取![]() 的中点
的中点![]() ,连接
,连接![]() ,根据中位线的方法证明四边形
,根据中位线的方法证明四边形![]() 是平行四边形.再证明
是平行四边形.再证明![]() 与
与![]() 从而证明
从而证明![]() 平面
平面![]() ,从而得到
,从而得到![]() 平面
平面![]() 即可.
即可.
(2) 以![]() 所在的直线为
所在的直线为![]() 轴建立空间直角坐标系,再求得平面
轴建立空间直角坐标系,再求得平面![]() 的法向量与平面
的法向量与平面![]() 的法向量进而求得二面角
的法向量进而求得二面角![]() 的余弦值即可.
的余弦值即可.
(1)证明:如图,取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
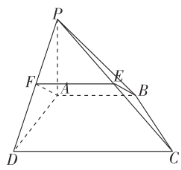
又![]() 为
为![]() 的中点,则
的中点,则![]() 是
是![]() 的中位线.所以
的中位线.所以![]() 且
且![]() .
.
又![]() 且
且![]() ,所以
,所以![]() 且
且![]() .所以四边形
.所以四边形![]() 是平行四边形.
是平行四边形.
所以![]() .因为
.因为![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
因为![]() ,所以
,所以![]() .因为
.因为![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .所以
.所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .又
.又![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)易知![]() 两两互相垂直,所以分别以
两两互相垂直,所以分别以![]() 所在的直线为
所在的直线为![]() 轴建立如图所示的空间直角坐标系:
轴建立如图所示的空间直角坐标系:
因为![]() ,所以点
,所以点![]() .
.
则![]() .设平面
.设平面![]() 的法向量为
的法向量为![]() ,
,
由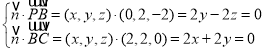 ,得
,得![]() ,
,
令![]() ,得平面
,得平面![]() 的一个法向量为
的一个法向量为![]() ;显然平面
;显然平面![]() 的一个法向量为
的一个法向量为![]() ;
;
设二面角![]() 的大小为
的大小为![]() ,则
,则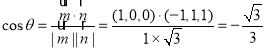 .
.
故二面角![]() 的余弦值是
的余弦值是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,且经过点
,且经过点 .
.
(1)求椭圆C的标准方程;
(2)过右焦点F的直线l与椭圆C相交于A,B两点,点B关于x轴的对称点为H,试问![]() 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①将一组数据中的每个数据都加上或减去同一个常数后,均值与方差都不变;②将某校参加摸底测试的1200名学生编号为1,2,3,…,1200,从中抽取一个容量为50的样本进行学习情况调查,按系统抽样的方法分为50组,如果第一组中抽出的学生编号为20,则第四组中抽取的学生编号为92;③线性回归方程![]() 必经过点
必经过点![]() ;④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有
;④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有![]() 的把握认为吸烟与患肺病有关系时,我们说现有100人吸烟,那么其中有99人患肺病.其中错误的个数是( )
的把握认为吸烟与患肺病有关系时,我们说现有100人吸烟,那么其中有99人患肺病.其中错误的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P–ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且![]() .
.
(Ⅰ)求证:CD⊥平面PAD;
(Ⅱ)求二面角F–AE–P的余弦值;
(Ⅲ)设点G在PB上,且![]() .判断直线AG是否在平面AEF内,说明理由.
.判断直线AG是否在平面AEF内,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来随着我国在教育科研上的投入不断加大,科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.伴随着国内市场增速放缓,国内有实力企业纷纷进行海外布局,第二轮企业出海潮到来.如在智能手机行业,国产品牌已在赶超国外巨头,某品牌手机公司一直默默拓展海外市场,在海外共设30多个分支机构,需要国内公司外派大量80后、90后中青年员工.该企业为了解这两个年龄层员工是否愿意被外派工作的态度,按分层抽样的方式从80后和90后的员工中随机调查了100位,得到数据如下表:
愿意被外派 | 不愿意被外派 | 合计 | |
80后 | 20 | 20 | 40 |
90后 | 40 | 20 | 60 |
合计 | 60 | 40 | 100 |
(1)根据调查的数据,是否有99%的把握认为“是否愿意被外派与年龄有关”,并说明理由;
(2)该公司举行参观驻海外分支机构的交流体验活动,拟安排6名参与调查的80后、90后员工参加.80后员工中有愿意被外派的3人和不愿意被外派的3人报名参加,从中随机选出3人,记选到愿意被外派的人数为![]() ;90后员工中有愿意被外派的4人和不愿意被外派的2人报名参加,从中随机选出3人,记选到愿意被外派的人数为
;90后员工中有愿意被外派的4人和不愿意被外派的2人报名参加,从中随机选出3人,记选到愿意被外派的人数为![]() ,求
,求![]() 的概率.
的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(参考公式: ,其中
,其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).
).
(1)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求以
,求以![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:①在回归模型中,预报变量y的值不能由解释变量x唯一确定;②若变量x,y满足关系![]() ,且变量y与z正相关,则x与z也正相关;③在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;④以模型
,且变量y与z正相关,则x与z也正相关;③在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;④以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() ,
,![]() .
.
其中真命题的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,试问在
,试问在![]() 轴上是否存在定点
轴上是否存在定点![]() 使得直线
使得直线![]() 与直线
与直线![]() 恰关于
恰关于![]() 轴对称?若存在,求出点
轴对称?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com