练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在一次运动会上，某单位派出了有6名主力队员和5名替补队员组成的代表队参加比赛.如果随机抽派5名队员上场比赛，将主力队员参加比赛的人数记为X，求随机变量X的概率分布以及随机变量X数学期望；（本题结果用分数表示即可）
    解：依题意知，抽取r个主力队员的概率为,r＝0,1,2,3,4,5.
    随机变量X的分布列为            
    X
    		0
    		1
    		2
    		3
    		4
    		5







    ∵X服从超几何分布  ∴随机变量X的数学期望E（X）＝＝  
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    对某班级50名同学一年来参加社会实践的次数进行的调查统计，得到如下频率分布表：
    参加次数
    		0
    		1
    		2
    		3
    人数
    		0.1
    		0．2
    		0.4
    		0.3
    根据上表信息解答以下问题：
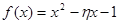    (1)从该班级任选两名同学，用η表示这两人参加社会实践次数之和，记“函数在区间，内有零点”的事件为，求发生的概率；
    (2)从该班级任选两名同学，用ξ表示这两人参加社会实践次数之差的绝对值，求随机变量ξ的分布列及数学期望Eξ

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    张先生家住H小区，他工作在C科技园区，从家开车到公司上班路上有L1，L2两条路线（如图），L1路线上有A1，A2，A3三个路口，各路口遇到红灯的概率均为；L2路线上有B1，B2两个路口，各路口遇到红灯的概率依次为，．
    （Ⅰ）若走L1路线，求最多遇到1次红灯的概率；
    （Ⅱ）若走L2路线，求遇到红灯次数的数学期望；
    （Ⅲ）按照“平均遇到红灯次数最少”的要求，请你帮助张先生分析上述两条路线中，选择
    哪条上班路线更好些，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    甲、乙、丙三人按下面的规则进行乒乓球比赛：第一局由甲、乙参加而丙轮空，以后每一局由前一局的获胜者与轮空者进行比赛，而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为，且各局胜负相互独立.求：
    （1）打了两局就停止比赛的概率；
    （2）打满3局比赛还未停止的概率；
    （3）比赛停止时已打局数的分布列与期望.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）一射击测试每人射击三次，每击中目标一次记10分。没有击中记0分，某人每次击中目标的概率为
    （I）求此人得20分的概率；（II）求此人得分的数学期望与方差。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    把一根长度为8的铁丝截成3段。
    （1）     若三段的长度均为整数，求三段的长度能构成三角形的概率；
    （2）     若把铁丝截成2,2,4的三段放入一盒子中，然后有放回地摸4次，设摸到长度为2的铁丝的次数为求与  

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    如果数据x1,x2,x3,…,xn的平均数为 ,方差为62，则数据3x1+5,3x2+5,…,3xn+5的平均数和方差分别是（   ）
    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    因冰雪灾害，某柑橘基地果林严重收损，为此有关专家提出一种拯救果树的方案，该方案需分两年实施且相互独立。该方案预计第一年可以使柑橘产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.2、0.4、0.4；第二年可以使柑橘产量为第一年的1.5倍、1.25倍、1.0倍的概率分别是0.3、0.3、0.4,求两年后柑橘产量恰好达到灾前产量的概率.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设随机变量ξ～B(2，p)，η～B(4，p)，若P(ξ≥1)＝，则P(η≥2)的值为-------（  ）
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案