
分析 an+an-1=$\frac{n}{{a}_{n}-{a}_{n-1}}$+2(n≥2),取分母化为:$({a}_{n}-1)^{2}$-$({a}_{n-1}-1)^{2}$=n.利用“累加求和”可得$({a}_{n}-1)^{2}$,再利用“裂项求和”方法即可得出.
解答 解:∵an+an-1=$\frac{n}{{a}_{n}-{a}_{n-1}}$+2(n≥2),
∴${a}_{n}^{2}-{a}_{n-1}^{2}$=n+2(an-an-1),
化为:$({a}_{n}-1)^{2}$-$({a}_{n-1}-1)^{2}$=n.
∴$({a}_{n}-1)^{2}$=[$({a}_{n}-1)^{2}$-$({a}_{n-1}-1)^{2}$]+[$({a}_{n-1}-1)^{2}$-$({a}_{n-2}-1)^{2}]$+…+$[({a}_{2}-1)^{2}-({a}_{1}-1)^{2}]$+$({a}_{1}-1)^{2}$
=n+(n-1)+…+2+1=$\frac{n(n+1)}{2}$.
∴$\frac{1}{({a}_{n}-1)^{2}}$=$\frac{2}{n(n+1)}$=2$(\frac{1}{n}-\frac{1}{n+1})$.
∴$\frac{1}{({a}_{1}-1)^{2}}$+$\frac{1}{({a}_{2}-1)^{2}}$+…+$\frac{1}{({a}_{n}-1)^{2}}$=2$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})]$
=2$(1-\frac{1}{n+1})$=$\frac{2n}{n+1}$.
故答案为:$\frac{2n}{n+1}$.
点评 本题考查了数列递推关系、“累加求和”方法、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:选择题
| A. | M∩N=M | B. | M∪(∁UN)=U | C. | M∩(∁UN)=∅ | D. | M⊆∁UN |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
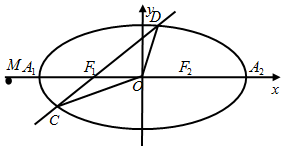 (文科)如图,已知椭圆的中心在坐标原点,焦点F1,F2,在x轴上,长轴A1A2的长为4,x轴上一点M(${-\frac{a^2}{c},0}$),$|{\overrightarrow{M{A_1}}}|$=$2|{\overrightarrow{{A_1}{F_1}}}|$.
(文科)如图,已知椭圆的中心在坐标原点,焦点F1,F2,在x轴上,长轴A1A2的长为4,x轴上一点M(${-\frac{a^2}{c},0}$),$|{\overrightarrow{M{A_1}}}|$=$2|{\overrightarrow{{A_1}{F_1}}}|$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com