Question

19．在△ABC中，$tanC=\frac{4}{3}$，$\overrightarrow{AH}•\overrightarrow{BC}=0$，$\overrightarrow{AB}•（\overrightarrow{CA}+\overrightarrow{CB}）=0$，H在BC边上，则过点B以A、H为两焦点的双曲线的离心率为$\frac{\sqrt{5}+1}{2}$．

Answer 1

分析 由△ABC中tanC=$\frac{4}{3}$，根据向量垂直的数量积为0，易得△ABC是等腰三角形，AH为腰上高，
由此设出各边的长度，然后根据双曲线的性质及双曲线离心率的定义，即可求出答案．

解答 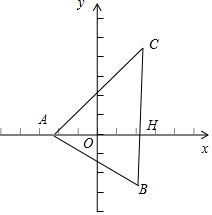解：如图所示；
△ABC中，$\overrightarrow{AH}•\overrightarrow{BC}=0$，
∴AH为BC边上的高；
又$\overrightarrow{AB}•（\overrightarrow{CA}+\overrightarrow{CB}）=0$，
∴CA=CB；
又tanC=$\frac{4}{3}$，令AH=4X，则CH=3X，
AC=CB=5X，BH=2X，
∴AB=$\sqrt{{（4X）}^{2}{+（2X）}^{2}}$=2$\sqrt{5}$X；
∴过点B以A、H为两焦点的双曲线中
2a=BA-BH=2（$\sqrt{5}$-1）X，
2c=AH=4X；
∴过点B以A、H为两焦点的双曲线的离心率为
e=$\frac{c}{a}$=$\frac{4X}{2（\sqrt{5}-1）X}$=$\frac{\sqrt{5}+1}{2}$．
故答案为：$\frac{{\sqrt{5}+1}}{2}$．

点评 本题考查了双曲线的简单性质，根据已知求出满足条件的△ABC形状进而求出各边长是解答本题的关键．