
分析 本题考查的知识点是几何概型的意义,关键是要找出sinθ>0对应线段的长度,再将其代入几何概型计算公式进行求解即得结果.
解答 解:θ∈[0,π],区间长度为π,
$sin({θ+\frac{π}{3}})>\frac{1}{2}$,$\frac{π}{6}$$<θ+\frac{π}{3}$<$\frac{5π}{6}$,∵θ∈[0,π],∴θ∈[0,$\frac{1}{2}$π],对应的区间长度为$\frac{1}{2}$π,
根据几何概型计算公式可得“$sin({θ+\frac{π}{3}})>\frac{1}{2}$”的概率是$\frac{1}{2}$.
故答案为:$\frac{1}{2}$
点评 几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.


科目:高中数学 来源: 题型:选择题
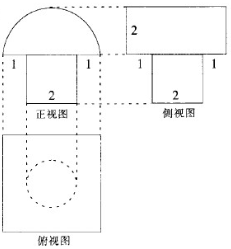
| A. | 20+17π | B. | 20+16π | C. | 16+17π | D. | 16+l6π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 销售量(件) | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 周数 | 2 | 4 | 8 | 13 | 13 | 8 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com