
分析 (I)求出C的焦点坐标为(±1,0),推出a,b,即可求解椭圆方程.
(II)设A(x1,y1),P(x2,y2)(x1≠x2),则$B({-{x_1},-{y_1}}),\;N({x_1},\frac{y_1}{2})$,利用平方差法求解${k_{BN}}=\frac{{\frac{3}{2}{y_1}}}{{2{x_1}}}=\frac{3}{4}•\frac{y_1}{x_1}$,${k_{BP}}=\frac{{{y_1}+{y_2}}}{{{x_1}+{x_2}}}$.利用B,N,P三点共线,所以kBN=kBP,转化求解即可.
解答 解:(I)由题意知,C的焦点坐标为(±1,0),…(1分)
$2a=\sqrt{{2^2}+{{(\frac{3}{2})}^2}}+\sqrt{0+{{(\frac{3}{2})}^2}}=\frac{5}{2}+\frac{3}{2}=4$,$b=\sqrt{3}$.…(3分)
所以,椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(4分)
(II)设A(x1,y1),P(x2,y2)(x1≠x2),则$B({-{x_1},-{y_1}}),\;N({x_1},\frac{y_1}{2})$
由点A,P在椭圆C上得,$\left\{\begin{array}{l}\frac{x_1^2}{4}+\frac{y_1^2}{3}=1\\ \frac{x_2^2}{4}+\frac{y_2^2}{3}=1\end{array}\right.$,两式相减得,$\frac{y_1^2-y_2^2}{x_1^2-x_2^2}=-\frac{3}{4}$.…(7分)
${k_{BN}}=\frac{{\frac{3}{2}{y_1}}}{{2{x_1}}}=\frac{3}{4}•\frac{y_1}{x_1}$,${k_{BP}}=\frac{{{y_1}+{y_2}}}{{{x_1}+{x_2}}}$.
因为B,N,P三点共线,所以kBN=kBP,即$\frac{y_1}{x_1}=\frac{4}{3}•\frac{{{y_1}+{y_2}}}{{{x_1}+{x_2}}}$.…(9分)
∴${k_{AB}}•{K_{AP}}=\frac{y_1}{x_1}•\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=\frac{4}{3}•\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}•\frac{{{y_1}+{y_2}}}{{{x_1}+{x_2}}}=\frac{4}{3}•\frac{y_1^2-y_1^2}{x_1^2-x_1^2}=-1$,为定值.…(12分)
点评 本题考查椭圆的简单性质的与,椭圆方程的求法,直线与椭圆的位置关系的综合应用,考查计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{32}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
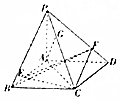 已知四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥平面ABCD,PA=AB=AC=2,AD=2$\sqrt{2}$,点E是线段AB上靠近B点的三等分点,点F、G分别在线段PD、PC上.
已知四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥平面ABCD,PA=AB=AC=2,AD=2$\sqrt{2}$,点E是线段AB上靠近B点的三等分点,点F、G分别在线段PD、PC上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
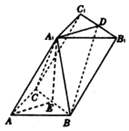 如图,在三棱柱ABC-A1B1C1中,D,E分别是B1C1、BC的中点,∠BAC=90°,AB=AC=2,A1A=4,A1E=$\sqrt{14}$.
如图,在三棱柱ABC-A1B1C1中,D,E分别是B1C1、BC的中点,∠BAC=90°,AB=AC=2,A1A=4,A1E=$\sqrt{14}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com