
【题目】某生物小组为了研究温度对某种酶的活性的影响进行了一组实验,得到的实验数据经整理得到如下的折线图:
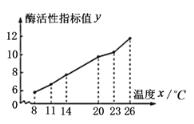
(1)由图可以看出,这种酶的活性![]() 与温度
与温度![]() 具有较强的线性相关性,请用相关系数加以说明;
具有较强的线性相关性,请用相关系数加以说明;
(2)求![]() 关于
关于![]() 的线性回归方程,并预测当温度为
的线性回归方程,并预测当温度为![]() 时,这种酶的活性指标值.(计算结果精确到0.01)
时,这种酶的活性指标值.(计算结果精确到0.01)
参考数据:![]() ,
,![]() ,
,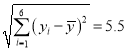 ,
,![]() .
.
参考公式:相关系数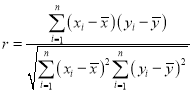 .
.
回归直线方程![]() ,
,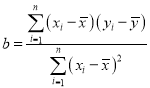 ,
,![]() .
.
 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①若样本数据![]() 的方差为
的方差为![]() ,则数据
,则数据![]() 的方差为
的方差为![]() ;
;
②“平面向量![]() 的夹角为锐角,则
的夹角为锐角,则![]() ”的逆命题为真命题;
”的逆命题为真命题;
③命题“![]() ,均有
,均有![]() ”的否定是“
”的否定是“![]() ,均有
,均有![]() ”;
”;
④![]() 是直线
是直线![]() 与直线
与直线![]() 平行的必要不充分条件.
平行的必要不充分条件.
其中正确的命题个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S一ABC中,SA=AB=AC=BC=![]() SB=
SB=![]() SC,O为BC的中点
SC,O为BC的中点
(1)求证:SO⊥平面ABC
(2)在线段AB上是否存在一点E,使二面角B—SC-E的平面角的余弦值为![]() ?若存在,求
?若存在,求![]() 的值,若不存在,试说明理由
的值,若不存在,试说明理由

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线![]() 和
和![]() 是异面直线,
是异面直线,![]() 在平面
在平面![]() 内,
内,![]() 在平面
在平面![]() 内,
内,![]() 是平面
是平面![]() 与平面
与平面![]() 的交线,则下列命题正确的是( )
的交线,则下列命题正确的是( )
A. ![]() 与
与![]() 都不相交 B.
都不相交 B. ![]() 与
与![]() 都相交
都相交
C. ![]() 至多与
至多与![]() 中的一条相交 D.
中的一条相交 D. ![]() 至少与
至少与![]() 中的一条相交
中的一条相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为A,若
的定义域为A,若![]() 且
且![]() 时总有
时总有![]() ,则称
,则称![]() 为单函数.例如,函数
为单函数.例如,函数![]() =2x+1(
=2x+1(![]() )是单函数.下列命题:
)是单函数.下列命题:
①函数![]() (x
(x![]() R)是单函数;
R)是单函数;
②指数函数![]() (x
(x![]() R)是单函数;
R)是单函数;
③若![]() 为单函数,
为单函数,![]() 且
且![]() ,则
,则![]() ;
;
④在定义域上具有单调性的函数一定是单函数.
其中的真命题是_________.(写出所有真命题的编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com