
| A. | $\frac{3}{4}$斗 | B. | $\frac{4}{5}$斗 | C. | 1斗 | D. | $\frac{5}{4}$斗 |
分析 利用率等差数列的通项公式列出方程组,求出首项和公差,由此能求出结果.
解答 解:由题意得:
$\left\{\begin{array}{l}{2{a}_{1}+{a}_{1}-{a}_{5}+{a}_{1}-2{a}_{5}+{a}_{1}-3{a}_{5}+{a}_{1}-4{a}_{5}=5}\\{{a}_{1}=-({a}_{1}+4d)}\end{array}\right.$,
解得${a}_{1}=\frac{5}{4},d=-\frac{1}{4}$,
∴6人中爵位为“簪裹”的人需献出栗的数量是a3=a1+2d=$\frac{5}{4}-\frac{2}{4}$=$\frac{3}{4}$(斗).
故选:A.
点评 本题考查了等差数列的通项公式,考查了等差数列的前n项和,是基础题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
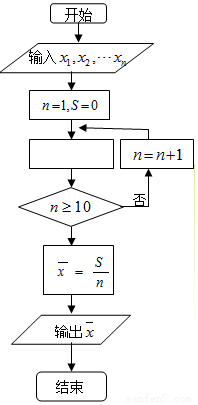 如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图,图中空白框中应填入的内容为( )
如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图,图中空白框中应填入的内容为( )| A. | S=S+xn | B. | S=S+$\frac{{x}_{n}}{n}$ | C. | S=S+n | D. | S=S+$\frac{{x}_{n}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 甲产品所需工时 | 乙产品所需工时 | |
| A设备 | 2 | 3 |
| B设备 | 4 | 1 |
| A. | 40万元 | B. | 45万元 | C. | 50万元 | D. | 55万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
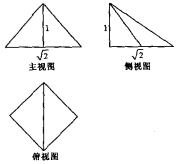 刘徽的《九章算术注》中有这样的记载:“邪解立方有两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”意思是说:把一块立方体沿斜线分成相同的两块,这两块叫做堑堵,再把一块堑堵沿斜线分成两块,大的叫阳马,小的叫鳖臑,两者体积比为2:1,这个比率是不变的,如图是一个阳马的三视图,则其表面积为( )
刘徽的《九章算术注》中有这样的记载:“邪解立方有两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”意思是说:把一块立方体沿斜线分成相同的两块,这两块叫做堑堵,再把一块堑堵沿斜线分成两块,大的叫阳马,小的叫鳖臑,两者体积比为2:1,这个比率是不变的,如图是一个阳马的三视图,则其表面积为( )| A. | 2 | B. | 2+$\sqrt{2}$ | C. | 3+$\sqrt{3}$ | D. | 3+$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 单调递减的 | B. | 单调递增的 | C. | 先增后减的 | D. | 先减后增的 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com