
| A. | 单调递减的 | B. | 单调递增的 | C. | 先增后减的 | D. | 先减后增的 |
分析 求出n=1时数列{an}的首项,再由当n≥2时,Tn-Tn-1,求得数列{an}的通项公式,再判断单调性,运用分子常数化或作差法,即可得到单调性.
解答 解:当n=1时,$\frac{1}{a_1}=\frac{1}{2}$,
解得a1=2.
当n≥2时,${T_n}-{T_{n-1}}=\frac{n}{a_n}=\frac{n^2}{2}-\frac{{{{({n-1})}^2}}}{2}=\frac{2n-1}{2}$,
所以${a_n}=\frac{2n}{2n-1}({n≥2})$,
综上有${a_n}=\frac{2n}{2n-1}=1+\frac{1}{2n-1}({n∈{N_+}})$,
所以a1>a2>a3>…,即数列{an}是单调递减的.
(或用${a_{n+1}}-{a_n}=\frac{-2}{{({2n+1})({2n-1})}}<0$).
故选A.
点评 本题考查数列的单调性的判断,注意运用数列的递推式求得数列的通项公式,考查化简整理的运算能力,属于中档题.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$斗 | B. | $\frac{4}{5}$斗 | C. | 1斗 | D. | $\frac{5}{4}$斗 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
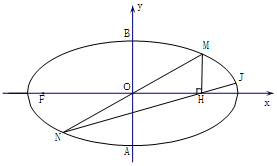 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点为F,短轴的两个端点分别为A、B,且|AB|=2,△ABF为等边三角形.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点为F,短轴的两个端点分别为A、B,且|AB|=2,△ABF为等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1]∪[3,+∞) | B. | (-∞,1)∪(3,+∞) | C. | [1,3] | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com