分析:(I)求导函数,分别求出k1和k2,计算k1•k2,可得k1•k2仅与a,b有关,与p无关;
(II)先确定A的坐标,代入曲线C1的方程,利用基本不等式,结合a2+b2取得最小值9,即可求曲线C1与抛物线C2的方程.
解答: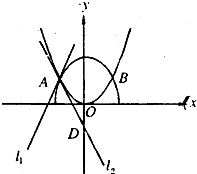
解:(I)设
A(x0,y0),由+=1(b>a>0,y≥0)得
y=,y′=-,
则
k1=y′|x=x0=-…(2分)
由
x2=2py(p>0)得y=,则
k2=y′|x=x0=,
所以
k1k2=-•=-,(※) …(4分)
又因为
=2py0,y0=,
则
=,即=.
代入(※)式得
k1k2=-=-•=-2()2.
可见,k
1•k
2仅与a,b有关,与p无关. …(6分)
(II)如图,设
A(x0,),则x0∈(-a,0)由(I)知
k2=,则l2:y=(x-x0)+.…(7分)
又
l2过点D(0,-2),则=4p,即x0=-2,
所以
A(-2,2)…(8分)
将点A的坐标代入曲线C
1的方程得
+=1.
则
a2+b2=(a2+b2)(+)=4p+4++≥4p+4+8,…(10分)
当且仅当“=”成立时,有
…(11分)
解得
所以C1:+=1(y≥0),C2:x2=.…(14分)
点评:本题考查曲线方程,考查直线与曲线的位置关系,考查学生分析解决问题的能力,属于中档题.

 (2009•枣庄一模)如图,曲线C1:
(2009•枣庄一模)如图,曲线C1: 解:(I)设A(x0,y0),由
解:(I)设A(x0,y0),由
