
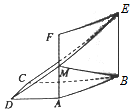
 如图所示,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四边形ABEF是正方形,且平面ABEF⊥平面ABCD,M为AF的中点,
如图所示,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四边形ABEF是正方形,且平面ABEF⊥平面ABCD,M为AF的中点,分析 (I)线线垂直转化为线面垂直,要证明AC⊥BM;只需证明BE⊥平面ABCD,即可.
(II)取BC的中点记为Q,BE的中点记为N,连接MN,QN,DQ,易得$CE∥QN,AB\underline{\underline∥}MN$.在直角梯形ABCD中,由BC=2AD=2DC可得$DQ\underline{\underline∥}AB$,所以四边形DMNQ为平行四边形,可得DM∥QN.故DM∥CE,∠DMB即为异面直线CE与BM所成的角(或其补角),利用余弦定理求解即可.
解答 解:(I)证明:∵四边形ABEF为正方形,∴BE⊥AB.
∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,BE?平面ABEF.
∴BE⊥平面ABCD.
∵AC?平面ABCD,∴BE⊥AC.
设AD=1,则$AC=AB=\sqrt{2}$,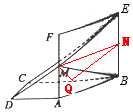
∴AC⊥AB且AB∩BE=B,
∴AC⊥平面ABEF,又BM?平面ABEF.∴AC⊥BM.
(II)取BC的中点记为Q,BE的中点记为N,连接MN,QN,DQ,
易得$CE∥QN,AB\underline{\underline∥}MN$.
在直角梯形ABCD中,由BC=2AD=2DC,
可得$DQ\underline{\underline∥}AB$,
∴四边形DMNQ为平行四边形,
可得DM∥QN.
故DM∥CE,
那么∠DMB即为异面直线CE与BM所成的角(或其补角)
设BC=2a,则AD=DC=a,
可得$DM=\frac{{\sqrt{6}}}{2}a,BD=\sqrt{5}a,BM=\frac{{\sqrt{10}}}{2}a$.$|{cos∠DMB}|=|{\frac{{({\frac{{\sqrt{10}}}{2}a})^2+{{({\frac{{\sqrt{6}}}{2}a})}^2}-{{({\sqrt{5a}})}^2}}}{{2×\frac{{\sqrt{10}}}{2}a×\frac{{\sqrt{6}}}{2}a}}}|=\frac{{\sqrt{15}}}{15}$.
得异面直线CE与BM所成角的余弦值为$\frac{{\sqrt{15}}}{15}$.
点评 本题考查空间点、线、面的位置关系及学生的空间想象能力、求两条异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | [3,4) | B. | (2,3] | C. | (1,2) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q | B. | p∧q | C. | ¬p∧q | D. | ¬p∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com