
| A. | $\frac{1}{12}$ | B. | $\frac{1}{24}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{6}$ |
分析 由b2=c-2c2>0得出c的范围,用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{BC}$,根据向量的数量级定义得出$\overrightarrow{BC}$•$\overrightarrow{AO}$关于c的函数.求出此函数的最大值即可.
解答 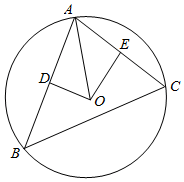 解:过OOD⊥AB于D,OE⊥AC于E,则D,E分别是AB,AC的中点.
解:过OOD⊥AB于D,OE⊥AC于E,则D,E分别是AB,AC的中点.
∴$\overrightarrow{BC}$•$\overrightarrow{AO}$=$\overrightarrow{AO}•(\overrightarrow{AC}-\overrightarrow{AB})$=$\overrightarrow{AO}•\overrightarrow{AC}$-$\overrightarrow{AO}•\overrightarrow{AB}$=AC•AE-AB•AD=$\frac{{b}^{2}-{c}^{2}}{2}$.
∵2c2-c+b2=0,∴b2=c-2c2>0,解得0$<c<\frac{1}{2}$.
∴$\overrightarrow{BC}•\overrightarrow{AO}$=$\frac{c-3{c}^{2}}{2}$=-$\frac{3}{2}$(c-$\frac{1}{6}$)2+$\frac{1}{24}$.
∴当c=$\frac{1}{6}$时,$\overrightarrow{BC}$•$\overrightarrow{AO}$取得最大值$\frac{1}{24}$.
故选B.
点评 本题考查了平面向量的数量级运算,二次函数的最值,属于中档题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:解答题
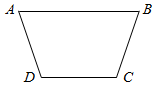 某地修建防洪渠道,其直截面图是等腰梯形ABCD(如图),底CD=40,腰AD=40,为使防洪渠道的通水量最大,应将防洪渠道的上口AB的宽设计为多少?
某地修建防洪渠道,其直截面图是等腰梯形ABCD(如图),底CD=40,腰AD=40,为使防洪渠道的通水量最大,应将防洪渠道的上口AB的宽设计为多少?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q是真命题 | B. | ¬p∨q是真命题 | C. | ¬q是假命题 | D. | p∧¬q是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{4}{3}$] | B. | [-2,$\frac{4}{3}$] | C. | [0,6] | D. | [-2,6] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com