
分析 讨论当x>0时,当x≤0时,分别运用指数函数和对数函数的单调性,解不等式,求得解集,再求并集,即可得到所求范围.
解答 解:当x>0时,f(x)≥2即为log${\;}_{\frac{1}{2}}$x≥2,
解得0<x≤$\frac{1}{4}$;
当x≤0时,f(x)≥2即为($\frac{1}{4}$)x≥2,
解得x≤-$\frac{1}{2}$.
综上可得,x的范围是(-∞,-$\frac{1}{2}$]∪(0,$\frac{1}{4}$].
故答案为:(-∞,-$\frac{1}{2}$]∪(0,$\frac{1}{4}$].
点评 本题考查分段函数的运用:解不等式,注意运用指数函数和对数函数的单调性,考查运算能力,属于中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{12}$ | B. | $\frac{1}{24}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
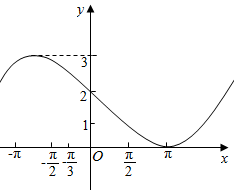 已知函数y=Asin(ωx+φ)+b(A>0,|φ|<π,b为常数)的一段图象(如图所示).
已知函数y=Asin(ωx+φ)+b(A>0,|φ|<π,b为常数)的一段图象(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com