考点:直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)要证平面AB1D⊥平面ABB1A1;只要证A1B⊥平面ADB1,根据直线与平面垂直的判定定理可知,只需证A1B与平面ADB1内两相交直线垂直,而AB1⊥A1B,AB1⊥DO,A1B∩DO=O,满足定理所需条件.
(2)连接CO并延长交AB于Q,则Q为AB的中点,连接CP,PQ,证明PC∥B1D,PQ∥B1A,利用面面平行的判定定理,可得平面PQC∥平面AB1D,即可证明OP∥平面AB1D.
解答:
证明:(1)连A
1B,与AB
1相交于E,连接DE,过C作CF⊥AB,则F为BC中点,
∵ABC-A
1B
1C
1是各条棱长均为a的正三棱柱,D是侧棱CC
1的中点,
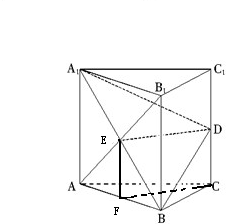
∴Rt△ACD≌Rt△B
1C
1D,∴AD=B
1D
又E是AB
1的中点,∴AB
1⊥DE,DE∥CF,
∴DE⊥AB,
∴DE⊥平面ABB
1A
1,DE?平面ADB
1,
∴平面AB
1D⊥平面ABB
1A
1;
(2)连接CO并延长交AB于Q,则Q为AB的中点,连接CP,PQ,
∵点D、P为棱CC
1、BB
1的中点,
∴PC∥B
1D,PQ∥B
1A,
∵PC∩PQ=P,B
1D∩B
1A=B
1,
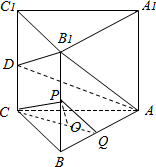
∴平面PQC∥平面AB
1D,
∵OP?平面PQC,
∴OP∥平面AB
1D.
点评:本题考查面面垂直的判定定理和线面平行判定定理的运用,数量运用判定定理是关键.

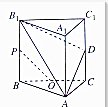 如图所示,ABC-A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点,P是B1B的中点,O是△ABC的中心,求证:
如图所示,ABC-A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点,P是B1B的中点,O是△ABC的中心,求证:



 (1)已知矩阵M=
(1)已知矩阵M=