考点:函数恒成立问题,函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:(1)由题意可得f(-x)+f(x)=0恒成立,故可得a=2,b=1或a=-2,b=-1,注意检验;
(2)由(1)可求得f(x)=
,利用定义证明即可;
(3)借助函数的性质化不等式f(log
m)+f(-1)>0为log
m<1,从而解得.
解答:
解:(1)由题意,
f(-x)+f(x)=
+
=0,
即(2
-x+1+a)(-2
x+b)+(-2
-x+b)(2
x+1+a)=0;
整理可得,
-2+2b2
-x-a2
x+ab-2+2b2
x-a2
-x+ab=0;
故
,
解得,a=2,b=1或a=-2,b=-1;
当a=-2,b=-1时,定义域不是R,故不成立;
故a=2,b=1;
(2)证明:由(1)知,f(x)=
;
任取x
1,x
2∈R,且x
1<x
2,
则f(x
1)-f(x
2)=
•
-
•
=
,
∵x
1<x
2,
∴0<
2x1<
2x2;
∴f(x
1)-f(x
2)>0;
故函数f(x)在R上是减函数;
(3)∵f(x)=
是R上的奇函数,
∴f(log
m)+f(-1)>0可化为f(log
m)>f(1);
又∵函数f(x)在R上是减函数;
故log
m<1;
①当m>1时,成立;
②当0<m<1时,
>m;
故0<m<
;
综上所述,m>1或0<m<
.
点评:本题考查了函数的性质的判断与证明,同时考查了恒成立问题,属于中档题.



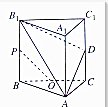 如图所示,ABC-A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点,P是B1B的中点,O是△ABC的中心,求证:
如图所示,ABC-A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点,P是B1B的中点,O是△ABC的中心,求证: