
【题目】如表是我国某城市在2017年1月份至10月份个月最低温与最高温(![]() )的数据一览表.
)的数据一览表.
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
最高温 | 5 | 9 | 9 | 11 | 17 | 24 | 27 | 30 | 31 | 21 |
最低温 |
|
|
|
|
|
|
|
|
|
|
已知该城市的各月最低温与最高温具有相关关系,根据这一览表,则下列结论错误的是( )
A.最低温与最高位为正相关
B.每月最高温和最低温的平均值在前8个月逐月增加
C.月温差(最高温减最低温)的最大值出现在1月
D.1月至4月的月温差(最高温减最低温)相对于7月至10月,波动性更大
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】对于曲线C所在平面上的定点![]() ,若存在以点
,若存在以点![]() 为顶点的角
为顶点的角![]() ,使得
,使得![]() 对于曲线C上的任意两个不同的点A,B恒成立,则称角
对于曲线C上的任意两个不同的点A,B恒成立,则称角![]() 为曲线C相对于点
为曲线C相对于点![]() 的“界角”,并称其中最小的“界角”为曲线C相对于点
的“界角”,并称其中最小的“界角”为曲线C相对于点![]() 的“确界角”.曲线
的“确界角”.曲线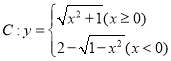 相对于坐标原点
相对于坐标原点![]() 的“确界角”的大小是 _________.
的“确界角”的大小是 _________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆O上除A,B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB=1,AB=4.

(1)证明:平面ADE⊥平面ACD;
(2)当C点为半圆的中点时,求二面角D﹣AE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某民航部门统计的2019年春运期间12个城市售出的往返机票的平均价格以及相比上年同期变化幅度的数据统计图表如图所示,根据图表,下面叙述不正确的是( )
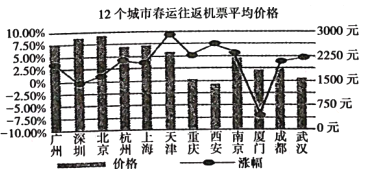
A. 同去年相比,深圳的变化幅度最小且厦门的平均价格有所上升
B. 天津的平均价格同去年相比涨幅最大且2019年北京的平均价格最高
C. 2019年平均价格从高到低居于前三位的城市为北京、深圳、广州
D. 同去年相比,平均价格的涨幅从高到低居于前三位的城市为天津、西安、南京
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验,受其启发,我们也可以通过设计下面的实验来估计π的值,先请240名同学,每人随机写下两个都小于1的正实数x,y组成的实数对(x,y);若将(x,y)看作一个点,再统计点(x,y)在圆x2+y2=1外的个数m;最后再根据统计数m来估计π的值,假如统计结果是m=52,那么可以估计π的近似值为_______.(用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,侧面SCD为钝角三角形且垂直于底面ABCD,![]() ,点M是SA的中点,
,点M是SA的中点,![]() ,
,![]() ,
,![]() .
.
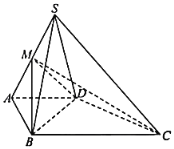
(1)求证:![]() 平面SCD;
平面SCD;
(2)若直线SD与底面ABCD所成的角为![]() ,求平面MBD与平面SBC所成的锐二面角的余弦值.
,求平面MBD与平面SBC所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为利于分层教学,某学校根据学生的情况分成了![]() ,
,![]() ,
,![]() 三类,经过一段时间的学习后在三类学生中分别随机抽取了1个学生的5次考试成绩,其统计表如下:
三类,经过一段时间的学习后在三类学生中分别随机抽取了1个学生的5次考试成绩,其统计表如下:
![]() 类
类
第 | 1 | 2 | 3 | 4 | 5 |
分数 | 145 | 83 | 95 | 72 | 110 |
![]() ,
,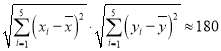 ;
;
![]() 类
类
第 | 1 | 2 | 3 | 4 | 5 |
分数 | 85 | 93 | 90 | 76 | 101 |
![]() ,
,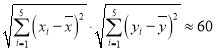 ;
;
![]() 类
类
第 | 1 | 2 | 3 | 4 | 5 |
分数 | 85 | 92 | 101 | 100 | 112 |
![]() ,
,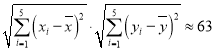 ;
;
(1)经计算已知![]() ,
,![]() 的相关系数分别为
的相关系数分别为![]() ,
,![]() ,请计算出
,请计算出![]() 学生的
学生的![]() 的相关系数,并通过数据的分析回答抽到的哪类学生学习成绩最稳定;(结果保留三位有效数字,
的相关系数,并通过数据的分析回答抽到的哪类学生学习成绩最稳定;(结果保留三位有效数字,![]() 越大认为成绩越稳定);
越大认为成绩越稳定);
(2)利用(1)中成绩最稳定的学生的样本数据,已知线性回归方程为![]() ,利用线性回归方程预测该生第九次的成绩.
,利用线性回归方程预测该生第九次的成绩.
参考公式:(1)样本![]() 的相关系数
的相关系数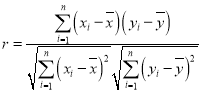 ;
;
(2)对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为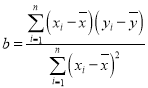 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系
轴的正半轴为极轴建立极坐标系![]() ,极坐标系中
,极坐标系中![]() ,弧
,弧![]() 所在圆的圆心分别为
所在圆的圆心分别为![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() .
.
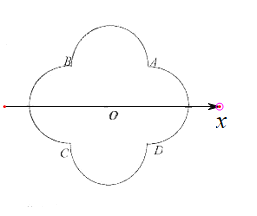
(1)分别写出![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),点
为参数),点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 有两个不同交点
有两个不同交点![]() ,求实数
,求实数![]() 的取值范围,并求出
的取值范围,并求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com