
| A. | 5035 | B. | 5039 | C. | 5043 | D. | 5047 |
分析 由an=$\sqrt{5n-1}$(n∈N*),n∈N*,可得此数列为$\sqrt{4}$,$\sqrt{9}$,$\sqrt{14}$,$\sqrt{19}$,$\sqrt{24}$,$\sqrt{29}$,$\sqrt{34}$,$\sqrt{39}$,$\sqrt{44}$,$\sqrt{49}$,$\sqrt{54}$,$\sqrt{59}$,$\sqrt{64}$,….可得an的整数项为:$\sqrt{4}$,$\sqrt{9}$,$\sqrt{49}$,$\sqrt{64}$,$\sqrt{144}$,$\sqrt{169}$,….即整数:2,3,7,8,12,13,….其规律就是各项之间是+1,+4,+1,+4,+1,+4这样递增的,可得其通项公式.
解答 解:由an=$\sqrt{5n-1}$(n∈N*),n∈N*,可得此数列为$\sqrt{4}$,$\sqrt{9}$,$\sqrt{14}$,$\sqrt{19}$,$\sqrt{24}$,$\sqrt{29}$,$\sqrt{34}$,$\sqrt{39}$,$\sqrt{44}$,$\sqrt{49}$,$\sqrt{54}$,$\sqrt{59}$,$\sqrt{64}$,….
an的整数项为:$\sqrt{4}$,$\sqrt{9}$,$\sqrt{49}$,$\sqrt{64}$,$\sqrt{144}$,$\sqrt{169}$,….
即整数:2,3,7,8,12,13,….
其规律就是各项之间是+1,+4,+1,+4,+1,+4这样递增的,
∴b2n-1=2+5(n-1)=5n-3,
b2n=3+5(n-1)=5n-2.
由2n=2018,解得n=1009,
∴b2018=5×1009-2=5043.
故选:C.
点评 本题考查了递推式的应用、观察分析猜想归纳数列通项公式、等差数列的通项公式,考查了推理能力与计算能力,属于中档题.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
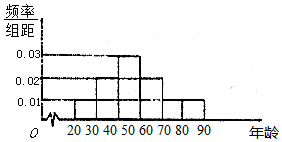 退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势,某机构为了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在20~80岁(含20岁和80岁)之间的600人进行调查,并按年龄层次绘制频率分布直方图,如图所示,若规定年龄分布在60~80岁(含60岁和80岁)为“老年人”.
退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势,某机构为了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在20~80岁(含20岁和80岁)之间的600人进行调查,并按年龄层次绘制频率分布直方图,如图所示,若规定年龄分布在60~80岁(含60岁和80岁)为“老年人”.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -2 | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ? | B. | 0 | C. | {0} | D. | {-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|1<x<3} | C. | {x|2<x<3} | D. | {x|x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com