
【题目】双曲线![]() 绕坐标原点
绕坐标原点![]() 旋转适当角度可以成为函数
旋转适当角度可以成为函数![]() 的图象,关于此函数
的图象,关于此函数![]() 有如下四个命题:①
有如下四个命题:① ![]() 是奇函数;②
是奇函数;② ![]() 的图象过点
的图象过点![]() 或
或![]() ;③
;③ ![]() 的值域是
的值域是![]() ;④ 函数
;④ 函数![]() 有两个零点;则其中所有真命题的序号为________.
有两个零点;则其中所有真命题的序号为________.
【答案】①②
【解析】
根据双曲线关于坐标原点对称,则旋转后得到的函数的![]() 图象也关于原点对称,即有
图象也关于原点对称,即有![]() 为奇函数;根据双曲线的顶点、渐近线方程可得旋转后的
为奇函数;根据双曲线的顶点、渐近线方程可得旋转后的![]() 的图象的渐近线,再由对称性可得
的图象的渐近线,再由对称性可得![]() 的图象过
的图象过![]() 或
或![]() ;根据
;根据![]() 的图象按逆时针旋转
的图象按逆时针旋转![]() 位于一三象限由图象可得顶点为点,不是极值点,则
位于一三象限由图象可得顶点为点,不是极值点,则![]() 的值域不是
的值域不是![]() ,也不是
,也不是
![]() ;分
;分![]() 的图象所在的象限讨论,得出
的图象所在的象限讨论,得出![]() 的图象与直线
的图象与直线![]() 没有交点,函数
没有交点,函数![]() 没有零点.
没有零点.
解:双曲线![]() 关于坐标原点对称,
关于坐标原点对称,
可得旋转后得到的函数的![]() 图象关于原点对称,
图象关于原点对称,

即有![]() 为奇函数,故①对;
为奇函数,故①对;
由双曲线的顶点为![]() ,渐近线方程为
,渐近线方程为![]() ,
,
可得![]() 的图象的渐近线为
的图象的渐近线为![]() 和
和![]() ,
,
图象关于直线![]() 对称,
对称,
可得![]() 的图象过
的图象过 或
或 .
.
由对称性可得![]() 的图象按逆时针
的图象按逆时针![]() 旋转位于—三象限;
旋转位于—三象限;
按顺时针旋转![]() 位于二四象限;故②对;
位于二四象限;故②对;
![]() 的图象按逆时针旋转
的图象按逆时针旋转![]() 位于一三象限由图象可得顶点为点
位于一三象限由图象可得顶点为点 或
或 ..
..
不是极值点,则![]() 的值域不是
的值域不是![]() ;
;
![]() 的图象按顺时针旋转
的图象按顺时针旋转![]() 位于二四象限,由对称性可得
位于二四象限,由对称性可得![]() 的值域也不是
的值域也不是
![]() ,故③不对;
,故③不对;
当![]() 的图象位于一三象限时,
的图象位于一三象限时,![]() 的图象与直线
的图象与直线![]() 有两个交点,函数
有两个交点,函数![]() 有两个零点;
有两个零点;
当![]() 的图象位于二四象限时,
的图象位于二四象限时,![]() 的图象与直线
的图象与直线![]() 没有交点,函数
没有交点,函数![]() 没有零点故④错.
没有零点故④错.
故真命题为:①②
故答案为:①②


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为满足人们的阅读需求,图书馆设立了无人值守的自助阅读区,提倡人们在阅读后将图书分类放回相应区域.现随机抽取了某阅读区500本图书的分类归还情况,数据统计如下(单位:本).
文学类专栏 | 科普类专栏 | 其他类专栏 | |
文学类图书 | 100 | 40 | 10 |
科普类图书 | 30 | 200 | 30 |
其他图书 | 20 | 10 | 60 |
(1)根据统计数据估计文学类图书分类正确的概率![]() ;
;
(2)根据统计数据估计图书分类错误的概率![]() ;
;
(3)假设文学类图书在“文学类专栏”、“科普类专栏”、“其他类专栏”的数目分别为![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,当
,当![]() ,
,![]() ,
,![]() 的方差
的方差![]() 最大时,求
最大时,求![]() ,
,![]() 的值,并求出此时方差
的值,并求出此时方差![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,若
的中点,若![]() 为线段
为线段![]() 上的动点(不含
上的动点(不含![]() ).
).
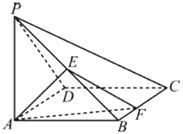
(1)平面![]() 与平面
与平面![]() 是否互相垂直?如果是,请证明;如果不是,请说明理由;
是否互相垂直?如果是,请证明;如果不是,请说明理由;
(2)求二面角![]() 的余弦值的取值范围.
的余弦值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=![]() ,O为AC与BD的交点,E为棱PB上一点.
,O为AC与BD的交点,E为棱PB上一点.

(1)证明:平面EAC⊥平面PBD;
(2)若PD∥平面EAC,求三棱锥P-EAD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有五个命题:
①函数![]() 的最小正周期是
的最小正周期是![]() ;
;
②终边在![]() 轴上的角的集合是
轴上的角的集合是![]() ;
;
③在同一坐标系中,函数![]() 的图象和函数
的图象和函数![]() 的图象有三个公共点;
的图象有三个公共点;
④把函数![]() 的图象向右平移
的图象向右平移![]() 个单位得到
个单位得到![]() 的图象;
的图象;
⑤函数![]() 在
在![]() 上是减函数;
上是减函数;
其中真命题的序号是( )
A.①②⑤B.①④C.③⑤D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年1月1日新修订的个税法正式实施,规定:公民全月工资、薪金所得不超过5000元的部分不必纳税,超过5000元的部分为全月应纳税所得额.此项税款按下表分段累计计算(预扣):
全月应缴纳所得额 | 税率 |
不超过3000元的部分 |
|
超过3000元至12000元的部分 |
|
超过12000元至25000元的部分 |
|
国家在实施新个税时,考虑到纳税人的实际情况,实施了《个人所得税税前专项附加扣税暂行办法》,具体如下表:
项目 | 每月税前抵扣金额(元) | 说明 |
子女教育 | 1000 | 一年按12月计算,可扣12000元 |
继续教育 | 400 | 一年可扣除4800元,若是进行技能职业教育或者专业技术职业资格教育一年可扣除3600元 |
大病医疗 | 5000 | 一年最高抵扣金额为60000元 |
住房贷款利息 | 1000 | 一年可扣除12000元,若夫妻双方在同一城市工作,可以选择一方来扣除 |
住房租金 | 1500/1000/800 | 扣除金额需要根据城市而定 |
2000 | 一年可扣除24000元,若不是独生子女,子女平均扣除.赡养老人年龄需要在60周岁及以上 |
老李本人为独生子女,家里有70岁的老人需要赡养,有一个女儿正读高三,他每月还需缴纳住房贷款2734元.若2019年11月老李工资,薪金所得为20000元,按照《个人所得税税前专项附加扣税暂行办法》,则老李应缴纳税款(预扣)为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数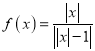 ,给出以下四个命题:(1)当
,给出以下四个命题:(1)当![]() 时,
时,![]() 单调递减且没有最值;(2)方程
单调递减且没有最值;(2)方程![]() 一定有实数解;(3)如果方程
一定有实数解;(3)如果方程![]() (
(![]() 为常数)有解,则解得个数一定是偶数;(4)
为常数)有解,则解得个数一定是偶数;(4)![]() 是偶函数且有最小值.其中假命题的序号是____________.
是偶函数且有最小值.其中假命题的序号是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集为![]() ,
,![]() ,定义集合
,定义集合![]() 的特征函数为
的特征函数为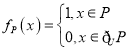 ,对于
,对于![]() ,
,![]() ,给出下列四个结论:
,给出下列四个结论:
(1)对任意![]() ,有
,有![]()
(2)对任意![]() ,若
,若![]() ,则
,则![]()
(3)对任意![]() ,有
,有![]()
(4)对任意![]() ,有
,有![]()
其中,正确的序号是_____
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数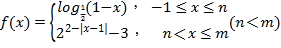 的值域是
的值域是![]() ,有下列结论:①当
,有下列结论:①当![]() 时,
时,![]() ; ②当
; ②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]() ; ④当
; ④当![]() 时,
时,![]() .其中结论正确的所有的序号是( ).
.其中结论正确的所有的序号是( ).
A.①②B.③④C.②③D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com