
【题目】某超市从现有甲、乙两种酸奶的日销售量(单位:箱)的1200个数据(数据均在区间![]() 内)中,按照5%的比例进行分层抽样,统计结果按
内)中,按照5%的比例进行分层抽样,统计结果按![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组,整理如下图:
分组,整理如下图:
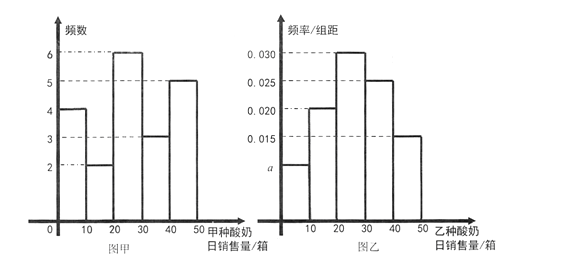
(Ⅰ)写出频率分布直方图(图乙)中![]() 的值;记所抽取样本中甲种酸奶与乙种酸奶日销售量的方差分别为
的值;记所抽取样本中甲种酸奶与乙种酸奶日销售量的方差分别为![]() ,
, ![]() ,试比较
,试比较![]() 与
与![]() 的大小(只需写出结论);
的大小(只需写出结论);
(Ⅱ)从甲种酸奶日销售量在区间![]() 的数据样本中抽取3个,记在
的数据样本中抽取3个,记在![]() 内的数据个数为
内的数据个数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)估计1200个日销售量数据中,数据在区间![]() 中的个数.
中的个数.
【答案】(Ⅰ)![]() ,
, ![]() ;(Ⅱ)见解析;(Ⅲ)160个.
;(Ⅱ)见解析;(Ⅲ)160个.
【解析】试题分析:
(1)利用概率为1求得![]() 的值,然后比较
的值,然后比较![]() 的大小即可;
的大小即可;
(2)首先确定![]() 所有可能的取值,然后利用超几何分布概率公式求解概率,最后写出分布列即可即可
所有可能的取值,然后利用超几何分布概率公式求解概率,最后写出分布列即可即可
(3)分析所给数据,利用频率近似代替概率,然后利用古典概型相关结论即可求得最终结果.
试题解析:
(Ⅰ)由图(乙)知, ![]() 解得
解得![]() ,
, ![]() .
.
(Ⅱ)![]() 的所有可能取值1,2,3.
的所有可能取值1,2,3.
则![]() ,
, ![]() ,
, ![]() ,
,
其分布列如下:
| 1 | 2 | 3 |
|
|
|
|
(Ⅲ)由图(甲)知,甲种酸奶的数据共抽取![]() 个,
个,
其中有4个数据在区间![]() 内,
内,
又因为分层抽样共抽取了![]() 个数据,
个数据,
乙种酸奶的数据共抽取![]() 个,
个,
由(Ⅰ)知,乙种酸奶的日销售量数据在区间![]() 内的频率为0.1,
内的频率为0.1,
故乙种酸奶的日销售量数据在区间![]() 内有
内有![]() 个.
个.
故抽取的60个数据,共有![]() 个数据在区间
个数据在区间![]() 内.
内.
所以,在1200个数据中,在区间![]() 内的数据有160个.
内的数据有160个.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线;
处的切线;
(2)若函数![]() 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌手机销售商今年1,2,3月份的销售量分别是1万部,1.2万部,1.3万部,为估计以后每个月的销售量,以这三个月的销售为依据,用一个函数模拟该品牌手机的销售量y(单位:万部)与月份x之间的关系,现从二次函数![]() 或函数
或函数![]() 中选用一个效果好的函数行模拟,如果4月份的销售量为1.37万件,则5月份的销售量为__________万件.
中选用一个效果好的函数行模拟,如果4月份的销售量为1.37万件,则5月份的销售量为__________万件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足下列条件:在定义域内存在
满足下列条件:在定义域内存在![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 具有性质
具有性质![]() ;反之,若
;反之,若![]() 不存在,则称函数
不存在,则称函数![]() 不具有性质
不具有性质![]() .
.
(Ⅰ)证明:函数![]() 具有性质
具有性质![]() ,并求出对应的
,并求出对应的![]() 的值;
的值;
(Ⅱ)试分别探究形如①![]() (
(![]() )、②
)、②![]() (
(![]() 且
且![]() )、③
)、③![]() (
(![]() 且
且![]() )的函数,是否一定具有性质
)的函数,是否一定具有性质![]() ?并加以证明.
?并加以证明.
(Ⅲ)已知函数![]() 具有性质
具有性质![]() ,求
,求![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】编号为A,B,C,D,E的5个小球放在如图所示的5个盒子里,要求每个盒子只能放1个小球,且A球不能放在1,2号盒子里,B球必须放在与A球相邻的盒子中,求不同的放法有多少种?
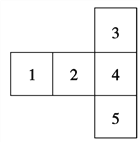
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某校新、老校区之间开车单程所需时间为![]() ,
, ![]() 只与道路畅通状况有关,对其容量为
只与道路畅通状况有关,对其容量为![]() 的样本进行统计,结果如图:
的样本进行统计,结果如图:
| 25 | 30 | 35 | 40 |
频数(次) | 20 | 30 | 40 | 10 |
(1)求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com