
对于函数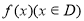 ,若
,若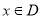 时,恒有
时,恒有 成立,则称函数
成立,则称函数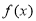 是
是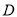 上 的“
上 的“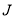 函数”.
函数”.
(Ⅰ)当函数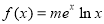 是定义域上的“
是定义域上的“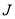 函数”时,求实数
函数”时,求实数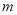 的取值范围;
的取值范围;
(Ⅱ)若函数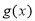 为
为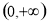 上的“
上的“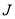 函数”.
函数”.
(ⅰ)试比较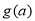 与
与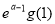 的大小(其中
的大小(其中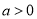 );
);
(ⅱ)求证:对于任意大于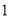 的实数
的实数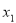 ,
,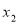 ,
,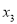 ,,
,,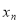 均有
均有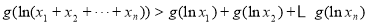 .
.
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源:2014-2015学年江西省六校高三3月联考文科数学试卷(解析版) 题型:填空题
设点P(x, y)为函数y=x2-2(x>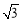 )图像上一动点,记m=
)图像上一动点,记m= , 则当m取最小值时,点P的坐标为 .
, 则当m取最小值时,点P的坐标为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省武汉市毕业生二月调研测试理科数学试卷(解析版) 题型:选择题
10件产品中有3件次品,不放回地抽取2次,在第1次抽出的是次品的前提下,则第2次抽出正品的概率是
A.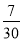 B.
B.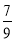 C.
C.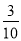 D.
D.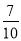
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省等高三上学期三校联考文科数学试卷(解析版) 题型:解答题
某市为调研高三一轮复习质量,在2014年10月份组织了一次摸底考试,并从某校2015届高三理科学生在该次考试的数学成绩进行分析,利用分层抽样抽取90分以上的1200名学生的成绩进行分析,已知该样本的容量为20,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:
分数段(分) | |
|
|
频数 | 4 | ||
频率 | | 0.45 | 0.2 |

(Ⅰ)求表中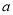 的值及分数在
的值及分数在 范围内的学生人数;
范围内的学生人数;
(Ⅱ)从得分在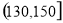 内的学生随机选2名学生的得分,求2名学生的平均分不低于140分的概率.
内的学生随机选2名学生的得分,求2名学生的平均分不低于140分的概率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省等高三上学期三校联考理科数学试卷(解析版) 题型:解答题
已知函数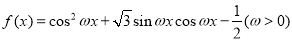 的最小正周期为
的最小正周期为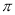 .
.
(I)求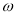 值及
值及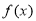 的单调递增区间;
的单调递增区间;
(II)在△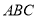 中,
中,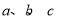 分别是三个内角
分别是三个内角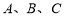 所对边,若
所对边,若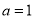 ,
,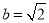 ,
,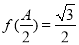 ,求
,求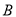 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2015年东北三省四市教研联合体高考模拟试卷(一)理科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-4:坐标系与参数方程
已知在直角坐标系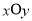 中,圆锥曲线
中,圆锥曲线 的参数方程为
的参数方程为 (
( 为参数),定点
为参数),定点 ,
, 是圆锥曲线
是圆锥曲线 的左、右焦点.
的左、右焦点.
(1)以坐标原点为极点, 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 且平行于直线
且平行于直线 的直线
的直线 的极坐标方程;
的极坐标方程;
(2)设(1)中直线 与圆锥曲线
与圆锥曲线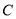 交于
交于 两点,求
两点,求 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com